题目内容
今年我市体育中考的现场选测项目中有一项是“排球30秒对墙垫球”,为了了解某学校九年级学生此项目平时的训练情况,随机抽取了该校部分九年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表:
(1)填空:a= ,b= ;
(2)这个样本数据的中位数在第 组;
(3)下表为《体育与健康》中考察“排球30秒对墙垫球”的中考评分标准,若该校九年级有550名学生,请你估计该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有多少人?
| 组别 | 垫球个数x(个) | 频数(人数) | 频率 |
| 1 | 10≤x<20 | 5 | 0.10 |
| 2 | 20≤x<30 | a | 0.18 |
| 3 | 30≤x<40 | 20 | b |
| 4 | 40≤x<50 | 16 | 0.32 |
| 合计 | 1.00 |
(2)这个样本数据的中位数在第
(3)下表为《体育与健康》中考察“排球30秒对墙垫球”的中考评分标准,若该校九年级有550名学生,请你估计该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有多少人?
| 排球30秒对墙垫球的中考评分标准 | ||||||||||
| 分值 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 排球(个) | 40 | 36 | 33 | 30 | 27 | 23 | 19 | 15 | 11 | 7 |
考点:频数(率)分布表,用样本估计总体,中位数
专题:
分析:(1)首先计算出总人数,再根据总数×频率=频数可得a,再根据频率=频数÷总数可得b;
(2)根据中位数的定义可得答案;
(3)首先计算出样本中得分在7分以上(包括7分)的人数所占百分比,再根据样本估计总体的方法可得答案.
(2)根据中位数的定义可得答案;
(3)首先计算出样本中得分在7分以上(包括7分)的人数所占百分比,再根据样本估计总体的方法可得答案.
解答:解:(1)总人数:5÷0.10=50,
a=50×0.18=9;
b=20÷50=0.40;
故答案为:a=9,b=0.40;
(2)根据中位数定义可得:位置处于中间的数在第3组;
(3)550×
=396(人).
答:该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有396人.
a=50×0.18=9;
b=20÷50=0.40;
故答案为:a=9,b=0.40;
(2)根据中位数定义可得:位置处于中间的数在第3组;
(3)550×
| 20+16 |
| 50 |
答:该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有396人.
点评:此题主要考查了中位数、样本估计总体、频数分布表,以及用样本估计总体,关键是掌握将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.频率=频数÷总数,用样本估计整体让整体×样本的百分比即可.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
1克大米约50粒,如果每人每天浪费1粒大米,那么全国13亿人每天就要浪费大米约( )
| A、26千克 |
| B、2.6×102千克 |
| C、2.6×103千克 |
| D、2.6×104千克 |
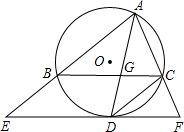 如图,已知⊙O为△ABC的外接圆,AD平分∠BAC交⊙O于D,过点D作EF∥BC分别交AB、AC延长线于点E、F.
如图,已知⊙O为△ABC的外接圆,AD平分∠BAC交⊙O于D,过点D作EF∥BC分别交AB、AC延长线于点E、F.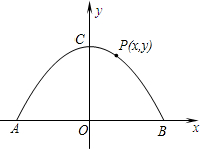 如图,二次函数y=-
如图,二次函数y=- 在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE,求证:BECF是正方形.
在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE,求证:BECF是正方形.