题目内容
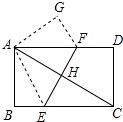 如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.
考点:矩形的性质,全等三角形的判定与性质,翻折变换(折叠问题)
专题:
分析:(1)由四边形ABCD是平行四边形与折叠性质,易得AB=AG,∠BAE=∠GAF,∠BEA=∠EAF=∠GFA,则可利用AAS判定:△ABE≌△AGF;
(2)据折叠的性质可得AE=EC,在直角△ABE中,根据勾股定理可列方程求得BE的长,则三角形的面积即可求得.
(2)据折叠的性质可得AE=EC,在直角△ABE中,根据勾股定理可列方程求得BE的长,则三角形的面积即可求得.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
由折叠的性质得:AG=CD,∠EAG=∠BCD,
∴AB=AG,∠BAD=∠EAG,
∴∠BAE=∠GAF,
又∵AB∥CD,AE∥GF,AD∥BC,
∴∠BEA=∠EAF=∠GFA,
在△ABE和△AGF中,
,
∴△ABE≌△AGF(AAS);
(2)解:根据折叠的性质可得AE=EC,
设BE=x,则AE=EC=8-x,
在直角△ABE中,根据勾股定理可得62+x2=(8-x)2,
解得:x=
,
则S△ABE=
AB•BE=
×6×
=
.
∴AB=CD,∠BAD=∠BCD,
由折叠的性质得:AG=CD,∠EAG=∠BCD,
∴AB=AG,∠BAD=∠EAG,
∴∠BAE=∠GAF,
又∵AB∥CD,AE∥GF,AD∥BC,
∴∠BEA=∠EAF=∠GFA,
在△ABE和△AGF中,
|
∴△ABE≌△AGF(AAS);
(2)解:根据折叠的性质可得AE=EC,
设BE=x,则AE=EC=8-x,
在直角△ABE中,根据勾股定理可得62+x2=(8-x)2,
解得:x=
| 7 |
| 4 |
则S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
| 21 |
| 4 |
点评:此题考查了平行四边形的性质、菱形的判定、折叠的性质以及全等三角形的判定与性质.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
相关题目
 如图,二次函数y=-
如图,二次函数y=-
 如图,在矩形ABCD中,点E在AB边上,点F在AD边上,且AE=DF,AF=CD,连接线段CE、EF、CF.点G是线段CE的中点,点M是线段EF上一点,过点G作GN⊥GM,将CF于点N.
如图,在矩形ABCD中,点E在AB边上,点F在AD边上,且AE=DF,AF=CD,连接线段CE、EF、CF.点G是线段CE的中点,点M是线段EF上一点,过点G作GN⊥GM,将CF于点N.
 如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:
如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图: