题目内容
15.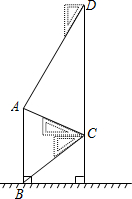 如图,中医药大学想把原来的校园内出现裂痕的李时珍的雕塑重新建造,为了和原来的高度一致,雕塑师小李为了测量其高度在教学楼二楼找到一点C,利用三角板测的雕塑顶端A点的仰角为30°,底部B点的俯角为45°,又在五楼找到一点D,利用三角板测得A点的俯角为60°.若CD为10米,求雕塑AB的高度(结果保留一位小数,$\sqrt{3}≈1.73$).
如图,中医药大学想把原来的校园内出现裂痕的李时珍的雕塑重新建造,为了和原来的高度一致,雕塑师小李为了测量其高度在教学楼二楼找到一点C,利用三角板测的雕塑顶端A点的仰角为30°,底部B点的俯角为45°,又在五楼找到一点D,利用三角板测得A点的俯角为60°.若CD为10米,求雕塑AB的高度(结果保留一位小数,$\sqrt{3}≈1.73$).
分析 过点C作CE⊥AB于E,根据已知条件得出AC=$\frac{1}{2}$CD,在Rt△ACE中,根据∠AEC=90°,∠ACE=30°,得出AE=$\frac{1}{2}$AC,再根据特殊角的三角函数值求出CE,
在Rt△BCE中,再根据∠BCE=45°,求出BE=CE=$\frac{5}{2}$$\sqrt{3}$,最后根据AB=AE+BE,即可得出答案.
解答 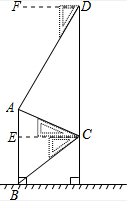 解:过点C作CE⊥AB于E,
解:过点C作CE⊥AB于E,
∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=10,
∴AC=$\frac{1}{2}$CD=5.
在Rt△ACE中,
∵∠AEC=90°,∠ACE=30°,
∴AE=$\frac{1}{2}$AC=$\frac{5}{2}$,
CE=AC•cos∠ACE=5•cos30°=$\frac{5}{2}$$\sqrt{3}$.
在Rt△BCE中,
∵∠BCE=45°,
∴BE=CE=$\frac{5}{2}$$\sqrt{3}$,
∴AB=AE+BE=$\frac{5}{2}$+$\frac{5}{2}$$\sqrt{3}$≈6.8(米).
答:雕塑AB的高度约为6.8米.
点评 此题考查了解直角三角形的应用-仰角俯角,要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.某班组织观看电影《1942》,现有甲、乙两种电影票,甲种票每张24元,乙种票每张18元,已知全班35名同学购票共用750元,那么甲乙两种电影票各( )张.
| A. | 20、15 | B. | 15、20 | C. | 25、10 | D. | 10、25 |
4.若分式$\frac{x-2y}{x+y}$中的x、y的值都变为原来的3倍,则此分式的值( )
| A. | 是原来的3倍 | B. | 不变 | C. | 是原来的$\frac{1}{3}$ | D. | 不能确定 |