Question

4．如图，∠ACE是△ABC的外角，BD平分∠ABC，CD平分∠ACE，BD和CD交于点D．
（1）∠A=40°时，求∠D的度数．
（2）∠A=90°时，求∠D的度数．

Answer 1

分析 （1）先根据角平分线定义得到∠ACE=2∠1，∠ABC=2∠2，再根据三角形外角性质得∠ACE=∠ABC+∠A，则2∠1=2∠2+∠A，接着再根据三角形外角性质得∠1=∠2+∠D，易得∠A=2∠D，即∠D=$\frac{1}{2}$∠A，进而得出答案；
（2）先根据角平分线定义得到∠ACE=2∠1，∠ABC=2∠2，再根据三角形外角性质得∠ACE=∠ABC+∠A，则2∠1=2∠2+∠A，接着再根据三角形外角性质得∠1=∠2+∠D，易得∠A=2∠D，即∠D=$\frac{1}{2}$∠A，进而得出答案．

解答 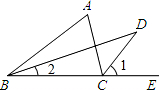解：如图，∵BD是△ABC的角平分线，CD是△ABC的外角∠ACE的平分线，
∴∠ACE=2∠1，∠ABC=2∠2，
∵∠ACE=∠ABC+∠A，
∴2∠1=2∠2+∠A，
而∠1=∠2+∠D，
∴2∠1=2∠2+2∠D，
∴∠A=2∠D，
即∠D=$\frac{1}{2}$∠A，
（1）当∠A=40°，则∠D=20°；
（2）若∠A=90°，则∠D=45°．

点评 本题考查了三角形内角和定理：三角形内角和是180°．主要用在求三角形中角的度数：①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．也考查了三角形外角性质．