题目内容
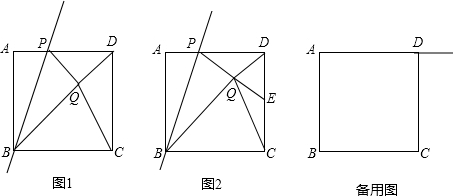
如图1.已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连结PQ、DQ、CQ、BQ,设AP=x.
(1)BQ+DQ的最小值是 .此时x的值是 .
(2)如图2,若PQ的延长线交CD边于点E,并且∠CQD=90°.
①求证:点E是CD的中点;②求x的值.
(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值.
(1)BQ+DQ的最小值是
(2)如图2,若PQ的延长线交CD边于点E,并且∠CQD=90°.
①求证:点E是CD的中点;②求x的值.
(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值.

考点:四边形综合题
专题:
分析:(1)BQ+DQ为点B到D两段折线的和.由两点间线段最短可知,连接DB,若Q点落在BD上,此时和最短,且为
.考虑动点运动,这种情形是存在的,由AP=x,则PD=1-x,PQ=x.又PDQ=45°,所以PD=
PQ,即1-x=
x.求解可得x=
-1.
(2)由已知条件对称分析,AB=BQ=BC,则∠BCQ=∠BQC,由∠BQE=∠BCE=90°,可得∠EQC=∠ECQ.那么若有QE=ED,则结论可证.再分析新条件∠CQD=90°,易得①结论.求x,通常都是考虑勾股定理,选择直角三角形PDE,发现PE,DE,PD都可用x来表示,进而易得方程,求解即可.
(3)若△CDQ为等腰三角形,则边CD比为改等腰三角形的一腰或者底边.又Q点为A点关于PB的对称点,则AB=QB,以点B为圆心,以AB的长为半径画弧,则Q点只能在弧AB上.若CD为腰,以点C为圆心,以CD的长为半径画弧,两弧交点即为使得△CDQ为等腰三角形(CD为腰)的Q点.若CD为底边,则作CD的垂直平分线,其与弧AC的交点即为使得△CDQ为等腰三角形(CD为底)的Q点.则如图所示共有三个Q点,那么也共有3个P点.作辅助线,利用直角三角形性质求之即可.
| 2 |
| 2 |
| 2 |
| 2 |
(2)由已知条件对称分析,AB=BQ=BC,则∠BCQ=∠BQC,由∠BQE=∠BCE=90°,可得∠EQC=∠ECQ.那么若有QE=ED,则结论可证.再分析新条件∠CQD=90°,易得①结论.求x,通常都是考虑勾股定理,选择直角三角形PDE,发现PE,DE,PD都可用x来表示,进而易得方程,求解即可.
(3)若△CDQ为等腰三角形,则边CD比为改等腰三角形的一腰或者底边.又Q点为A点关于PB的对称点,则AB=QB,以点B为圆心,以AB的长为半径画弧,则Q点只能在弧AB上.若CD为腰,以点C为圆心,以CD的长为半径画弧,两弧交点即为使得△CDQ为等腰三角形(CD为腰)的Q点.若CD为底边,则作CD的垂直平分线,其与弧AC的交点即为使得△CDQ为等腰三角形(CD为底)的Q点.则如图所示共有三个Q点,那么也共有3个P点.作辅助线,利用直角三角形性质求之即可.
解答:(1)答:
,
-1.
(2)①证明:在正方形ABCD中,
AB=BC,∠A=∠BCD=90°.
∵Q点为A点关于BP的对称点,
∴AB=QB,∠A=∠PQB=90°,
∴QB=BC,∠BQE=∠BCE,
∴∠BQC=∠BCQ,
∴∠EQC=∠EQB-∠CQB=∠ECB-∠QCB=∠ECQ,
∴EQ=EC.
在Rt△QDC中,
∵∠QDE=90°-∠QCE,
∠DQE=90°-∠EQC,
∴∠QDE=∠DQE,
∴EQ=ED,
∴CE=EQ=ED,即E为CD的中点.
②解:∵AP=x,AD=1,
∴PD=1-x,PQ=x,CD=1.
在Rt△DQC中,
∵E为CD的中点,
∴DE=QE=CE=
,
∴PE=PQ+QE=x+
,
∴(x+
)2=(1-x)2+(
)2,
解得 x=
.
(3)答:△CDQ为等腰三角形时x的值为2-
,
,2+
.
(分析如下:以下内容作答不要求书写)
如图,以点B为圆心,以AB的长为半径画弧,以点C为圆心,以CD的长为半径画弧,两弧分别交于Q1,Q3.此时△CDQ1,△CDQ3都为以CD为腰的等腰三角形.
作CD的垂直平分线交弧AC于点Q2,此时△CDQ2以CD为底的等腰三角形.

以下对此Q1,Q2,Q3.分别讨论各自的P点,并求AP的值.
①讨论Q1,如图作辅助线,连接BQ1、CQ1,作PQ1⊥BQ1交AD于P,过点Q1,作EF⊥AD于E,交BC于F.

∵△BCQ1为等边三角形,正方形ABCD边长为1,
∴Q1F=
,Q1E=
.
在四边形ABPQ1中,
∵∠ABQ1=30°,
∴∠APQ1=150°,
∴△PEQ1为含30°的直角三角形,
∴PE=
EQ1=
.
∵AE=
,
∴x=AP=AE-PE=2-
.
②讨论Q2,如图作辅助线,连接BQ2,AQ2,过点Q2作PG⊥BQ2,交AD于P,连接BP,过点Q2作EF⊥CD于E,交AB于F.

∵EF垂直平分CD,
∴EF垂直平分AB,
∴AQ2=BQ2.
∵AB=BQ2,
∴△ABQ2为等边三角形.
在四边形ABQP中,
∵∠BAD=∠BQP=90°,∠ABQ2=60°,
∴∠APE=120°
∴∠EQ2G=∠DPG=180°-120°=60°,
∴Q2E=
,
∴EG=
,
∴DG=DE+GE=
-1,
∴PD=1-
,
∴x=AP=1-PD=
.
③对Q3,如图作辅助线,连接BQ1,CQ1,BQ3,CQ3,过点Q3作BQ3⊥PQ3,交AD的延长线于P,连接BP,过点Q1,作EF⊥AD于E,此时Q3在EF上,不妨记Q3与F重合.

∵△BCQ1为等边三角形,△BCQ3为等边三角形,BC=1,
∴Q1Q2=
,Q1E=
,
∴EF=
.
在四边形ABQ3P中
∵∠ABF=∠ABC+∠CBQ3=150°,
∴∠EPF=30°,
∴EP=
EF=
.
∵AE=
,
∴x=AP=AE+PE=
+2.
综上所述,△CDQ为等腰三角形时x的值为2-
,
,2+
.
| 2 |
| 2 |
(2)①证明:在正方形ABCD中,
AB=BC,∠A=∠BCD=90°.
∵Q点为A点关于BP的对称点,
∴AB=QB,∠A=∠PQB=90°,
∴QB=BC,∠BQE=∠BCE,
∴∠BQC=∠BCQ,
∴∠EQC=∠EQB-∠CQB=∠ECB-∠QCB=∠ECQ,
∴EQ=EC.
在Rt△QDC中,
∵∠QDE=90°-∠QCE,
∠DQE=90°-∠EQC,
∴∠QDE=∠DQE,
∴EQ=ED,
∴CE=EQ=ED,即E为CD的中点.
②解:∵AP=x,AD=1,
∴PD=1-x,PQ=x,CD=1.
在Rt△DQC中,
∵E为CD的中点,
∴DE=QE=CE=
| 1 |
| 2 |
∴PE=PQ+QE=x+
| 1 |
| 2 |
∴(x+
| 1 |
| 2 |
| 1 |
| 2 |
解得 x=
| 1 |
| 3 |
(3)答:△CDQ为等腰三角形时x的值为2-
| 3 |
| ||
| 3 |
| 3 |
(分析如下:以下内容作答不要求书写)
如图,以点B为圆心,以AB的长为半径画弧,以点C为圆心,以CD的长为半径画弧,两弧分别交于Q1,Q3.此时△CDQ1,△CDQ3都为以CD为腰的等腰三角形.
作CD的垂直平分线交弧AC于点Q2,此时△CDQ2以CD为底的等腰三角形.

以下对此Q1,Q2,Q3.分别讨论各自的P点,并求AP的值.
①讨论Q1,如图作辅助线,连接BQ1、CQ1,作PQ1⊥BQ1交AD于P,过点Q1,作EF⊥AD于E,交BC于F.

∵△BCQ1为等边三角形,正方形ABCD边长为1,
∴Q1F=
| ||
| 2 |
2-
| ||
| 2 |
在四边形ABPQ1中,
∵∠ABQ1=30°,
∴∠APQ1=150°,
∴△PEQ1为含30°的直角三角形,
∴PE=
| 3 |
2
| ||
| 2 |
∵AE=
| 1 |
| 2 |
∴x=AP=AE-PE=2-
| 3 |
②讨论Q2,如图作辅助线,连接BQ2,AQ2,过点Q2作PG⊥BQ2,交AD于P,连接BP,过点Q2作EF⊥CD于E,交AB于F.

∵EF垂直平分CD,
∴EF垂直平分AB,
∴AQ2=BQ2.
∵AB=BQ2,
∴△ABQ2为等边三角形.
在四边形ABQP中,
∵∠BAD=∠BQP=90°,∠ABQ2=60°,
∴∠APE=120°
∴∠EQ2G=∠DPG=180°-120°=60°,
∴Q2E=
2-
| ||
| 2 |
∴EG=
2
| ||
| 2 |
∴DG=DE+GE=
| 3 |
∴PD=1-
| ||
| 3 |
∴x=AP=1-PD=
| ||
| 3 |
③对Q3,如图作辅助线,连接BQ1,CQ1,BQ3,CQ3,过点Q3作BQ3⊥PQ3,交AD的延长线于P,连接BP,过点Q1,作EF⊥AD于E,此时Q3在EF上,不妨记Q3与F重合.

∵△BCQ1为等边三角形,△BCQ3为等边三角形,BC=1,
∴Q1Q2=
| 3 |
2-
| ||
| 2 |
∴EF=
2+
| ||
| 2 |
在四边形ABQ3P中
∵∠ABF=∠ABC+∠CBQ3=150°,
∴∠EPF=30°,
∴EP=
| 3 |
2
| ||
| 2 |
∵AE=
| 1 |
| 2 |
∴x=AP=AE+PE=
| 3 |
综上所述,△CDQ为等腰三角形时x的值为2-
| 3 |
| ||
| 3 |
| 3 |
点评:本题第一问非常基础,难度较低.第二问因为动点的原因,思路不易找到,这里就需要做题时充分分析已知条件,尤其是新给出的条件.其中求边长是勾股定理的重要应用,是很重要的考点.第三问是一个难度非常高的题目,可以利用尺规作图的思想将满足要求的点Q找全.另外求解各个P点也是考察三角函数及勾股定理的综合应用,有着极高的难度.

练习册系列答案
相关题目
抛物线y=3x2向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )
| A、y=3(x-1)2-2 |
| B、y=3(x+1)2-2 |
| C、y=3(x+1)2+2 |
| D、y=3(x-1)2+2 |
若
是有理数,则x一定是( )
| x2 |
| A、正实数 | B、有理数 |
| C、正有理数 | D、完全平方数 |
 已知在正方形ABCD中,F在对角线AC上,BF⊥FE,且AF=CE=2,求正方形ABCD的面积.
已知在正方形ABCD中,F在对角线AC上,BF⊥FE,且AF=CE=2,求正方形ABCD的面积. 如图所示,在直角坐标系中,点E从O点出发,以1个单位/秒的速度沿x轴正方向运动,点F从O点出发,以2个单位/秒的速度沿y轴正方向运动,B(4,2),以BE为直径作⊙O1.
如图所示,在直角坐标系中,点E从O点出发,以1个单位/秒的速度沿x轴正方向运动,点F从O点出发,以2个单位/秒的速度沿y轴正方向运动,B(4,2),以BE为直径作⊙O1.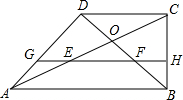 在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F.
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F. 