题目内容
 如图,DE是△ABC的中位线,求证:DE∥BC,且DE=
如图,DE是△ABC的中位线,求证:DE∥BC,且DE=| 1 |
| 2 |
考点:三角形中位线定理
专题:证明题
分析:延长DE到Q,使DE=EQ,连接CQ,根据SAS证△ADE≌△CQE,推出AD=CQ,∠A=∠ACQ,推出平行四边形DQCB,得出DQ=BC,DQ∥BC,即可推出答案.
解答: 证明:延长DE到Q,使DE=EQ,连接CQ,
证明:延长DE到Q,使DE=EQ,连接CQ,
∵AE=EC,∠AED=∠CEQ,DE=EQ,
∴△ADE≌△CQE,
∴AD=CQ,∠A=∠ACQ,
∴AB∥CQ,
∵AD=BD,
∴BD=CQ,
∴四边形DBCQ是平行四边形,
∴DQ=BC,DQ∥BC,
∴DE∥BC,DE=
BC.
 证明:延长DE到Q,使DE=EQ,连接CQ,
证明:延长DE到Q,使DE=EQ,连接CQ,∵AE=EC,∠AED=∠CEQ,DE=EQ,
∴△ADE≌△CQE,
∴AD=CQ,∠A=∠ACQ,
∴AB∥CQ,
∵AD=BD,
∴BD=CQ,
∴四边形DBCQ是平行四边形,
∴DQ=BC,DQ∥BC,
∴DE∥BC,DE=
| 1 |
| 2 |
点评:本题主要考查对平行四边形的性质和判定,平行线的判定,全等三角形的性质和判定,三角形的中位线等知识点的理解和掌握,能证出四边形DQCB是平行四边形是解此题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,AB是⊙O的直径,点C在圆上,P是AB延长线上一点,连结AC,PC,过点O作AC的垂线交AC于点D,交⊙O于点E.若AC=PC,AB=8,∠P=30°.
如图,AB是⊙O的直径,点C在圆上,P是AB延长线上一点,连结AC,PC,过点O作AC的垂线交AC于点D,交⊙O于点E.若AC=PC,AB=8,∠P=30°.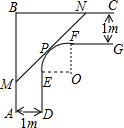 一走廊拐角的横截面积如图所示,已知AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊宽度都是1m,
一走廊拐角的横截面积如图所示,已知AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊宽度都是1m,
 如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x-y)的最大值是
如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x-y)的最大值是 如图,AC⊥BC于点C,DE⊥BE于点E,BC平分∠ABE,∠BDE=58°.则∠A=
如图,AC⊥BC于点C,DE⊥BE于点E,BC平分∠ABE,∠BDE=58°.则∠A= 如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=
如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=