题目内容
 如图,AB是⊙O的直径,点C在圆上,P是AB延长线上一点,连结AC,PC,过点O作AC的垂线交AC于点D,交⊙O于点E.若AC=PC,AB=8,∠P=30°.
如图,AB是⊙O的直径,点C在圆上,P是AB延长线上一点,连结AC,PC,过点O作AC的垂线交AC于点D,交⊙O于点E.若AC=PC,AB=8,∠P=30°.(1)求证:PC是⊙O的切线;
(2)求阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)根据AC=PC,∠P=30°,得∠CAO=30°,连接OC,可求得∠PCO=90°,即PC⊥OC,从而可证明PC是⊙O的切线;
(2)由AB=8,得AO=
AB,再由∠CAO=30°,OE⊥AC,得OD和CD的长,从而得出S阴影部分=S扇形OCE-S△OCD即可.
(2)由AB=8,得AO=
| 1 |
| 2 |
解答: (1)证明:∵AC=PC,∠P=30°,
(1)证明:∵AC=PC,∠P=30°,
∴∠CAO=30°,
连接OC.
∴∠COP=2∠CAO=60°,
∴∠PCO=180°-∠ACO-∠COP=90°,
即PC⊥OC,
∴PC是⊙O的切线;
(2)解:∵AB=8,
∴AO=
AB=4,
又∵∠CAO=30°,OE⊥AC
∴OD=
OA=2,CD=AD=
OA=2
,
∴S阴影部分=S扇形OCE-S△OCD=
π×42-
×2×2
=
π-2
.
 (1)证明:∵AC=PC,∠P=30°,
(1)证明:∵AC=PC,∠P=30°,∴∠CAO=30°,
连接OC.
∴∠COP=2∠CAO=60°,
∴∠PCO=180°-∠ACO-∠COP=90°,
即PC⊥OC,
∴PC是⊙O的切线;
(2)解:∵AB=8,
∴AO=
| 1 |
| 2 |
又∵∠CAO=30°,OE⊥AC
∴OD=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴S阴影部分=S扇形OCE-S△OCD=
| 60 |
| 360 |
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 3 |
点评:本题考查了切线的判定以及扇形面积的计算,是基础题,难度不大.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 如图,四边形ABCD中,AD=CD,连结BD.若不增加任何字母与辅助线,要使△ABD≌△CBD,则还需增加一个条件是
如图,四边形ABCD中,AD=CD,连结BD.若不增加任何字母与辅助线,要使△ABD≌△CBD,则还需增加一个条件是
 如图,DE是△ABC的中位线,求证:DE∥BC,且DE=
如图,DE是△ABC的中位线,求证:DE∥BC,且DE=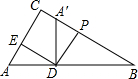 如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=3,DE⊥AC于点E,AE=1,若△ADE绕点D顺时针旋转90°后,点A、E的对应点A′、F恰好在BC边上,则A′C=
如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=3,DE⊥AC于点E,AE=1,若△ADE绕点D顺时针旋转90°后,点A、E的对应点A′、F恰好在BC边上,则A′C=