题目内容
 如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x-y)的最大值是
如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x-y)的最大值是考点:切线的性质
专题:几何图形问题,压轴题
分析:作直径AC,连接CP,得出△APC∽△PBA,利用
=
,得出y=
x2,所以x-y=x-
x2=-
x2+x=-
(x-4)2+2,当x=4时,x-y有最大值是2.
| AP |
| AC |
| BP |
| AP |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
解答:解:如图,作直径AC,连接CP,

∴∠CPA=90°,
∵AB是切线,
∴CA⊥AB,
∵PB⊥l,
∴AC∥PB,
∴∠CAP=∠APB,
∴△APC∽△PBA,
∴
=
,
∵PA=x,PB=y,半径为4,
∴
=
,
∴y=
x2,
∴x-y=x-
x2=-
x2+x=-
(x-4)2+2,
当x=4时,x-y有最大值是2,
故答案为:2.

∴∠CPA=90°,
∵AB是切线,
∴CA⊥AB,
∵PB⊥l,
∴AC∥PB,
∴∠CAP=∠APB,
∴△APC∽△PBA,
∴
| AP |
| AC |
| PB |
| PA |
∵PA=x,PB=y,半径为4,
∴
| x |
| 8 |
| y |
| x |
∴y=
| 1 |
| 8 |
∴x-y=x-
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
当x=4时,x-y有最大值是2,
故答案为:2.
点评:此题考查了切线的性质,平行线的性质,相似三角形的判定与性质,以及二次函数的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图几何体的主视图是( )
如图几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
 如图,DE是△ABC的中位线,求证:DE∥BC,且DE=
如图,DE是△ABC的中位线,求证:DE∥BC,且DE=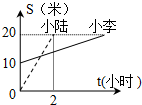 小李和小陆沿同一条路行驶到B地,他们离出发地的距离S和行驶时间t之间的函数关系的图象如图.已知小李离出发地的距离S和行驶时间t之间的函数关系为y=2x+10.则:
小李和小陆沿同一条路行驶到B地,他们离出发地的距离S和行驶时间t之间的函数关系的图象如图.已知小李离出发地的距离S和行驶时间t之间的函数关系为y=2x+10.则: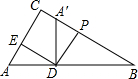 如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=3,DE⊥AC于点E,AE=1,若△ADE绕点D顺时针旋转90°后,点A、E的对应点A′、F恰好在BC边上,则A′C=
如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=3,DE⊥AC于点E,AE=1,若△ADE绕点D顺时针旋转90°后,点A、E的对应点A′、F恰好在BC边上,则A′C=