题目内容
8.下列四组数:①4,5,8;②7,24,25;③6,8,10;④$\sqrt{2}$,$\sqrt{2}$,2.其中可以为直角三角形三边长的有②③④.(把所有你认为正确的序号都写上)分析 根据勾股定理的逆定理可知,当三角形中三边的关系为:a2+b2=c2时,则三角形为直角三角形.据此可解本题.
解答 解:①∵42+52≠82,不能构成直角三角形;
②72+242=252,能构成直角三角形;
③62+82=102,能构成直角三角形;
④($\sqrt{2}$)2+($\sqrt{2}$)2=22,能构成直角三角形.
所以可以为直角三角形三边长的有②③④.
故答案为:②③④.
点评 此题考查勾股定理的逆定理的运用,掌握三边关系是判定一个三角形是否是直角三角形的关键.

练习册系列答案
相关题目
16. 如图,在?ABCD中,∠B=60°,则∠D的度数等于( )
如图,在?ABCD中,∠B=60°,则∠D的度数等于( )
 如图,在?ABCD中,∠B=60°,则∠D的度数等于( )
如图,在?ABCD中,∠B=60°,则∠D的度数等于( )| A. | 120° | B. | 60° | C. | 40° | D. | 30° |
 已知,如图,AB⊥CD,BE是⊙O的直径,
已知,如图,AB⊥CD,BE是⊙O的直径,
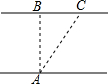 某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B,结果离欲到达点B 240米,已知他在水中游了510米,求该河的宽度(两岸可近似看做平行).
某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B,结果离欲到达点B 240米,已知他在水中游了510米,求该河的宽度(两岸可近似看做平行).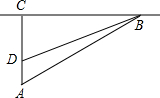 校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载,某中学九年级数学活动小组进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点A,在公路1上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米.已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒.
校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载,某中学九年级数学活动小组进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点A,在公路1上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米.已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒.