题目内容
3.甲经销商库存有1200套A牌服装,每套进价400元,售价500元,一年内可卖完.现市场流行B品牌服装,每套进价300元,售价600元,一年内B品牌服装销售无积压,但一年内只允许经销商一次性订购B品牌服装,因甲经销商无流动资金可用,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售,经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为y=-$\frac{1}{10}$x+360(100≤x≤1200),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).(1)求转让后剩余的A品牌服装的销售款Q1(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款Q2(元)与x(套)之间的函数关系式;
(3)求W(元)与x(套)之间的函数关系式,并求转让多少套时,所获总利润W最大,最大值是多少.
分析 (1)直接根据销售款=售价×套数即可得出结论;
(2)根据转让价格y(元/套)与转让数量x(套)之间的函数关系式为y=-$\frac{1}{10}$x+360(100≤x≤1200)得出总件数,再与售价相乘即可;
(3)把(1)(2)中的销售款相加再减去成本即可.
解答 解:(1)∵甲经销商库存有1200套A品牌服装,每套售价500元,转让x套给乙,
∴Q1=500×(1200-x)=-500x+600000(100≤x≤1200);
(2)∵转让价格y(元/套)与转让数量x(套)之间的函数关系式为y=-$\frac{1}{10}$x+360(100≤x≤1200),B品牌服装,每套进价300元,
∴转让后可购买B服装的套数=$\frac{x•(-\frac{1}{10}x+360)}{300}$元,
∴Q2=$\frac{x•(-\frac{1}{10}x+360)}{300}$×600=-$\frac{1}{5}$x2+720x(100≤x≤1200);
(3)∵由(1)、(2)知,Q1=-500x+600000,Q2=-$\frac{1}{5}$x2+720x,
∴W=Q1+Q2-400×1200=-500x+600000-$\frac{1}{5}$x2+720x-480000=-$\frac{1}{5}$(x-550)2+180500,
当x=550时,W有最大值,最大值为180450元.
点评 本题考查的是二次函数的应用,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
13.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.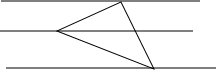 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
18. 如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
 如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )| A. | 70° | B. | 60° | C. | 40° | D. | 20° |
12.关于二次函数$y=-\frac{1}{2}{(x-1)^2}+2$的图象与性质,下列结论错误的是( )
| A. | 抛物线与x轴有两个交点 | B. | 当x=1时,函数有最大值 | ||
| C. | 抛物线可由$y=-\frac{1}{2}{x^2}$经过平移得到 | D. | 当-1<x≤2时,函数y的整数值有3个 |
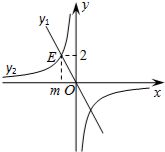 如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2).
如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2). 如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.