题目内容
12.关于二次函数$y=-\frac{1}{2}{(x-1)^2}+2$的图象与性质,下列结论错误的是( )| A. | 抛物线与x轴有两个交点 | B. | 当x=1时,函数有最大值 | ||
| C. | 抛物线可由$y=-\frac{1}{2}{x^2}$经过平移得到 | D. | 当-1<x≤2时,函数y的整数值有3个 |
分析 根据二次函数的性质对各小题分析判断即可得求解.
解答 解:A、∵a=-$\frac{1}{2}$<0,顶点(1,2),
∴抛物线与x轴有两个交点;
B、∵抛物线开口向下,顶点(1,2)∴当x=1时,函数有最大值2;
C、抛物线可由$y=-\frac{1}{2}{x^2}$向右平移1个单位,向上平移2个单位得到;
D、∵当-1<x≤2时,0<y≤2,∴函数y的整数值有1,2两个;
综上所述,结论错误的是D.
故选D.
点评 本题考查了二次函数的性质,主要利用了抛物线的开口方向、对称轴、顶点坐标,以及二次函数的增减性.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
20.下列说法正确的是( )
| A. | πx2y的系数是1 | B. | $\frac{1}{2}$xy2的次数是3 | ||
| C. | -27ab2的系数是27 | D. | $\frac{4abd}{3}$的系数是4 |

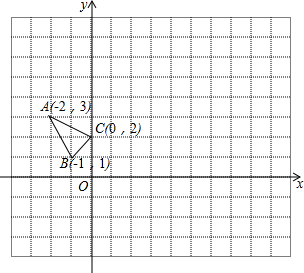 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示. 请你根据如图所示已知条件,推想正确结论,要求每个结论同时含有字母a,b.写出至少三条正确结论:b>a,ab>0,a+b<0.
请你根据如图所示已知条件,推想正确结论,要求每个结论同时含有字母a,b.写出至少三条正确结论:b>a,ab>0,a+b<0. 如图,二次函数y=(x-h)2+k的顶点坐标为M(1,-4).
如图,二次函数y=(x-h)2+k的顶点坐标为M(1,-4). 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为85°.
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为85°.