题目内容
18．
如图，已知AB=CD，BC=AD，∠B=20°，则∠D=（ ）| A． | 70° | B． | 60° | C． | 40° | D． | 20° |
分析 首先证明△BAC≌△DCA，再根据全等三角形对应边相等可得∠D=∠B．
解答 解：∵在△BAC和△DCA中$\left\{\begin{array}{l}{AB=CD}\\{AC=AC}\\{BC=AD}\end{array}\right.$，
∴△BAC≌△DCA（SSS），
∴∠D=∠B=20°，
故选：D．
点评 此题主要考查了全等三角形的判定和性质，关键是掌握全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．
练习册系列答案
相关题目
如图，线段MN表示一段高架道路，线段AB表示高架道路旁的一排居民楼．已知点A到MN的距离为15m，BA的延长线与MN相交于点D，且∠BDN=30°．若汽车沿着从M到N的方向在MN上行驶，方圆39m以内会受到噪音的影响，当其到达点P时，噪音开始影响这一排的居民楼；当其到达点Q时，它与这一排居民楼的距离为39m，求PQ的长度（精确到1m）（参考数据：$\sqrt{3}$≈1.7）
如图，⊙O为△ABC的外接圆，直线l与⊙O相切与点P，且l∥BC．
13．
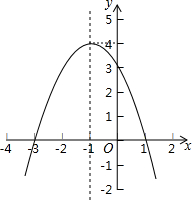已知抛物线y=ax2+bx+c如图所示，请结合图象中所给信息完成以下问题：
（1）求抛物线的表达式；
（2）若该抛物线经过一次平移后过原点O，请写出一种平移方法，并写出平移后得到的新抛物线的表达式．
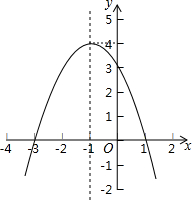已知抛物线y=ax2+bx+c如图所示，请结合图象中所给信息完成以下问题：（1）求抛物线的表达式；
（2）若该抛物线经过一次平移后过原点O，请写出一种平移方法，并写出平移后得到的新抛物线的表达式．
8．下表是二次函数y=ax2+bx+c（ a≠0）图象上部分点的横坐标（x）和纵坐标（y）．
（1）观察表格，直接写出m=3；
（2）其中A（x1，y1）、B（x2，y2）在函数的图象上，且-1＜x1＜0，2＜x2＜3，则y1＞y2（用“＞”或“＜”填空）；
（3）求这个二次函数的表达式．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | m | 8 | … |
（2）其中A（x1，y1）、B（x2，y2）在函数的图象上，且-1＜x1＜0，2＜x2＜3，则y1＞y2（用“＞”或“＜”填空）；
（3）求这个二次函数的表达式．