题目内容
5.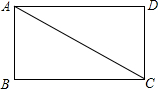 已知:如图,Rt△ABC≌Rt△CDA,其中点A,D的对应点分别是C,B,∠B=∠D=Rt∠.求证:四边形ABCD是矩形.
已知:如图,Rt△ABC≌Rt△CDA,其中点A,D的对应点分别是C,B,∠B=∠D=Rt∠.求证:四边形ABCD是矩形.
分析 由Rt△ABC≌Rt△CDA,根据全等三角形的对应角相等,可得∠BAC=∠ACD,又由∠B=∠D=Rt∠,即可证得∠BCD=90°,然后由有三个角是直角的四边形是矩形,证得结论.
解答 证明:∵Rt△ABC≌Rt△CDA,
∴∠BAC=∠ACD,
∵∠B=∠D=Rt∠,
∴∠BAC+∠ACB=90°,
∴∠ACB+∠ACD=90°,
即∠BCD=90°,
∴四边形ABCD是矩形.
点评 此题考查了矩形的判定以及全等三角形的性质.注意求得∠BCD=90°是关键.

练习册系列答案
相关题目
16.甲种糖果的单价是每千克20元,乙种糖果的单价是每千克15元,若要配制200千克单价为每千克18元的混合糖,并使之和分别销售两种糖果的总收入保持不变,问需甲、乙两种糖果各多少千克?
(1)填写下表:
(2)列出方程,作出解答.
(1)填写下表:
| 数量/千克 | 单价/(元/千克) | 销售收入/元 | |
| 甲种糖果 | x | 20 | 20x |
| 乙种糖果 | 200-x | 15 | 15(200-x) |
| 丙种糖果 | 200 | 18 | 200×18 |
13.在平面直角坐标系中.已知点A(4,0)点B(0,3).点P在x轴上,且△ABP为等腰三角形,则P点有( )个.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 已知:如图,在?ABCD中,对角线AC,BD相交于点O.∠1=∠2.求证:?ABCD是矩形.
已知:如图,在?ABCD中,对角线AC,BD相交于点O.∠1=∠2.求证:?ABCD是矩形. 已知:如图,CD是Rt△ABC的斜边AB上的高,用余弦、正切的定义证明:
已知:如图,CD是Rt△ABC的斜边AB上的高,用余弦、正切的定义证明: 如图,在直角坐标系中,O是坐标原点,已知△OAB的顶点A(-6,0),B(0,2),将△OAB绕点O按顺时针旋转90°,得到△ODC.
如图,在直角坐标系中,O是坐标原点,已知△OAB的顶点A(-6,0),B(0,2),将△OAB绕点O按顺时针旋转90°,得到△ODC.