题目内容
13.在平面直角坐标系中.已知点A(4,0)点B(0,3).点P在x轴上,且△ABP为等腰三角形,则P点有( )个.| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 分为三种情况:①AB=AP,②AP=BP,③AB=BP,画出图形,即可得出答案.
解答  解:∵A(4,0)点B(0,3),
解:∵A(4,0)点B(0,3),
∴AO=4,OB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
如图:
①以A为圆心,以AB为半径作弧,交x轴于P,AP1=AP4=5此时两点C1(-1,0),C4(9,0);
②当AP=BP时,此时点C在AB的垂直平分线上,P3($\frac{7}{8}$,0);
③以B为圆心,以AB为半径作弧,交x轴于P2,此时AB=BP,点C2(-4,0);
综上所述点C的坐标为:(-1,0)、(9,0)、(-4,0)、($\frac{7}{8}$,0).
故选C.
点评 本题考查了等腰三角形的判定,坐标与图形性质的应用,用了分类讨论思想.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
8.已知ax=ay,下列结论错误的是( )
| A. | x=y | B. | b+ax=b+ay | C. | ax-c=ay-c | D. | $\frac{ax}{5}$=$\frac{ay}{5}$ |
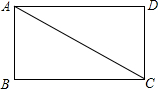 已知:如图,Rt△ABC≌Rt△CDA,其中点A,D的对应点分别是C,B,∠B=∠D=Rt∠.求证:四边形ABCD是矩形.
已知:如图,Rt△ABC≌Rt△CDA,其中点A,D的对应点分别是C,B,∠B=∠D=Rt∠.求证:四边形ABCD是矩形.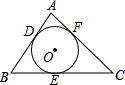 如图所示,⊙O分别切△ABC的三边AB、BC、CA于点D、E、F,若BC=10,AC=11,AB=8,求AF、BD、CE的长.
如图所示,⊙O分别切△ABC的三边AB、BC、CA于点D、E、F,若BC=10,AC=11,AB=8,求AF、BD、CE的长.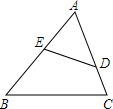 如图,D、E分别是△ABC的边AC、AB上的点,AD=6,AB=10,BC=12,且$\frac{AE}{AC}=\frac{3}{5}$,
如图,D、E分别是△ABC的边AC、AB上的点,AD=6,AB=10,BC=12,且$\frac{AE}{AC}=\frac{3}{5}$,