题目内容
7. 如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.
如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.
分析 作PM⊥AC.PN⊥B垂足分别为M、N,先证明△PND≌△PME,△PAN≌△PAM,可以得AD+AE=$\sqrt{3}$AP即可解决问题.
解答 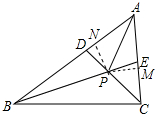 解:作PM⊥AC.PN⊥B垂足分别为M、N.
解:作PM⊥AC.PN⊥B垂足分别为M、N.
∵BE、CD分别平分∠ABC、∠ACB,
∴PA也是∠BAC的平分线,
∴PM=PN,
∵∠BAC=60°,
∴∠BPC=∠MPN=120°,
∴∠DPN=∠MPE,
在△PDN和△PEM中,
$\left\{\begin{array}{l}{∠DPN=∠MPE}\\{∠PND=∠PME}\\{PN=PM}\end{array}\right.$,
∴△PND≌△PME,
∴DN=EM,
在△APN和△APM中,
$\left\{\begin{array}{l}{PA=PA}\\{PN=PM}\end{array}\right.$,
∴△PAN≌△PAM,
∴AN=AM,
在RT△PAM中,∵∠PAM=30°,
∴AM=$\frac{\sqrt{3}}{2}$PA,
∴AD+AE=AN+DN+AM-EM=2AM=$\sqrt{3}$PA,
∵PA=1,
∴$AD+AE=\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查全等三角形的判定和性质、角平分线的性质、等边三角形的性质等知识,添加辅助线构造全等三角形是解决问题的关键,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在平面直角坐标系中,已知A(1,0),B(2015,0),点P是该平面直角坐标系内的一个动点,则使∠APB=30°的点P有( )
| A. | 0个 | B. | 2014个 | C. | 2015个 | D. | 无数个 |
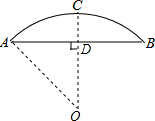 如图所示,已知AB=16m,半径OA=10m,高度CD为4m.
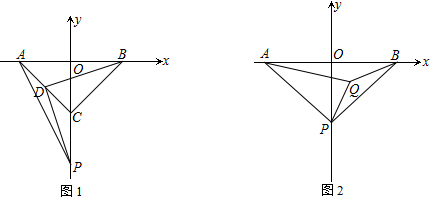
如图所示,已知AB=16m,半径OA=10m,高度CD为4m. 如图,矩形PABC的顶点P在抛物线y=-(x-1)2-2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.
如图,矩形PABC的顶点P在抛物线y=-(x-1)2-2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.