题目内容
15.若满足不等式$\frac{8}{15}<\frac{n}{n+k}<\frac{7}{13}$的整数k只有一个,则正整数n的最大值112.分析 对不等式进行变换把分子变成1,再根据分母越大数越小可得关于$\frac{k}{n}$的范围,再将两分数变成同分母,根据整数k只有一个可得n的值.
解答 解:对不等式进行变换,即分子变成1:$\frac{1}{1+\frac{7}{8}}<\frac{1}{1+\frac{k}{n}}<\frac{1}{1+\frac{6}{7}}$
分母越大,则数越小,所以有:$1+\frac{7}{8}>1+\frac{k}{n}$且1+$\frac{k}{n}$>1+$\frac{6}{7}$,
即:$\frac{6}{7}$<$\frac{k}{n}$<$\frac{7}{8}$,
变成同分母:$\frac{96}{112}<\frac{k}{n}<\frac{98}{112}$
∴整数k只有一个,
∴k=97,此时n=112.
故答案为:112.
点评 本题主要考查一元一次不等式组的应用、分式的值的问题,正确对分式进行转化是解决本题的关键.

练习册系列答案
相关题目
3.在火车站,通常可看到列车运行时刻表,T13列车由北京开往上海,T14列车由上海开往北京,这两次列车每天各发一列车,自北京到上海铁路线长1462km,请根据下表提供的信息进行分析:
北京与上海之间往返的T13、T14列车运行时刻表如下:
根据列车运行时刻表估算,T13与T14列车相遇地点距北京大约多远(铁路线长保留整数)?
北京与上海之间往返的T13、T14列车运行时刻表如下:
| 北京 | 天津西 | 济南 | 上海 | ||
| T13 | 到站时间 | … | 16:11 | 20:11 | 8:04 |
| 发车时间 | 14:40 | 16:16 | 20:23 | … | |
| T14 | 到站时间 | 9:03 | 7:23 | 3:14 | … |
| 发车时间 | … | 7:28 | 3:26 | 15:45 |
20.如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)=1,d(102)=2.
那么:d(103)=3,d(10-2)=-2
(2)劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d( $\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:
$\frac{d({a}^{3})}{d(a)}$=2d(a)(a为正数).
若d(3)=0.4771,则d(9)=0.9542,d($\frac{3}{10}$)=-0.5229;
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
(1)根据劳格数的定义,填空:d(10)=1,d(102)=2.
那么:d(103)=3,d(10-2)=-2
(2)劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d( $\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:
$\frac{d({a}^{3})}{d(a)}$=2d(a)(a为正数).
若d(3)=0.4771,则d(9)=0.9542,d($\frac{3}{10}$)=-0.5229;
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
| x | 0.8 | 2 | 3.2 | 4 | 5 | 8 |
| d(x) | 6a-3b+1 | 2a-b | 10a-5b | 4a-2b | 1-2a+b | 6a-3b |
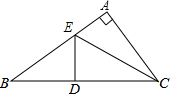 如图,在△ABC中,∠A=90°,DE垂直平分BC,求证:BE2-AE2=AC2.
如图,在△ABC中,∠A=90°,DE垂直平分BC,求证:BE2-AE2=AC2. 如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.
如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.