题目内容
19. 如图,矩形PABC的顶点P在抛物线y=-(x-1)2-2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.
如图,矩形PABC的顶点P在抛物线y=-(x-1)2-2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.
分析 显然当点P位于抛物线的顶点时,矩形的面积最小,从而确定两边的长,求得周长即可.
解答 解:抛物线y=-(x-1)2-2的顶点坐标为(1,-2),
当点P位于抛物线的顶点处时,PA=2,
∵PC=2PA,
∴PC=4,
∴周长的最小值为2×(2+4)=12,
故答案为:12.
点评 本题考查了二次函数的性质,解题的关键是了解当点P位于抛物线的顶点处时,矩形的周长最小,难度不大.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
8.在平面直角坐标系中,将点B(-3,2)向左平移5个单位长度,再向上平移3个单位长度后与点A(x,y)重合,则点A的坐标是( )
| A. | (2,5) | B. | (-8,5) | C. | (-8,-1) | D. | (2,-1) |
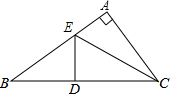 如图,在△ABC中,∠A=90°,DE垂直平分BC,求证:BE2-AE2=AC2.
如图,在△ABC中,∠A=90°,DE垂直平分BC,求证:BE2-AE2=AC2. 如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.
如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.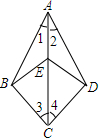 已知:如图,∠1=∠2,∠3=∠4.求证:∠AEB=∠AED.
已知:如图,∠1=∠2,∠3=∠4.求证:∠AEB=∠AED.