题目内容
1.在平面直角坐标系中,已知A(1,0),B(2015,0),点P是该平面直角坐标系内的一个动点,则使∠APB=30°的点P有( )| A. | 0个 | B. | 2014个 | C. | 2015个 | D. | 无数个 |
分析 已知点A、点B是定点,要使∠APB=30°,只需点P在过点A、点B的圆上,且弧AB所对的圆心角为60°即可.
解答 解:以AB为边,在第一象限内作等边三角形ABC,
以点C为圆心,AC为半径作⊙C,交y轴于点P1、P2.
在优弧AP1B上任取一点P,
则∠APB=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×60°=30°.
∴使∠APB=30°的点P有无数个.
故选:D.
点评 本题考查的是圆周角定理、坐标与图形的性质以及等边三角形的性质,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.

练习册系列答案
相关题目
3.在火车站,通常可看到列车运行时刻表,T13列车由北京开往上海,T14列车由上海开往北京,这两次列车每天各发一列车,自北京到上海铁路线长1462km,请根据下表提供的信息进行分析:
北京与上海之间往返的T13、T14列车运行时刻表如下:
根据列车运行时刻表估算,T13与T14列车相遇地点距北京大约多远(铁路线长保留整数)?
北京与上海之间往返的T13、T14列车运行时刻表如下:
| 北京 | 天津西 | 济南 | 上海 | ||
| T13 | 到站时间 | … | 16:11 | 20:11 | 8:04 |
| 发车时间 | 14:40 | 16:16 | 20:23 | … | |
| T14 | 到站时间 | 9:03 | 7:23 | 3:14 | … |
| 发车时间 | … | 7:28 | 3:26 | 15:45 |
8.在平面直角坐标系中,将点B(-3,2)向左平移5个单位长度,再向上平移3个单位长度后与点A(x,y)重合,则点A的坐标是( )
| A. | (2,5) | B. | (-8,5) | C. | (-8,-1) | D. | (2,-1) |
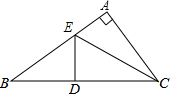 如图,在△ABC中,∠A=90°,DE垂直平分BC,求证:BE2-AE2=AC2.
如图,在△ABC中,∠A=90°,DE垂直平分BC,求证:BE2-AE2=AC2. 如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.
如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.