题目内容
11.蓬安特产“姚麻花”的成本价为每斤6元,某专卖店“姚麻花”的售价每斤15元,每天可卖出50斤.市场调查反映:如调整价格,每涨价1元,每天要少卖出10斤;每降价1元,每天可多卖出10斤.(1)如果专卖店卖“姚麻花”每天要想获得480元的利润,且要尽可能的让利给顾客,那么售价应定价多少元?
(2)请你帮专卖店老板算一算,如何定价才能使利润最大,并求出最大的利润?
分析 (1)设应涨价x元,利用每一个的利润×售出的个数=总利润,列出方程解答即可,再设降价y元,利用每一个的利润×售出的个数=总利润,列出方程解答即可;
(2)分两种情况探讨:涨价和降价,列出函数,利用配方法求得最大值,比较得出答案即可.
解答 解:(1)设售价应涨价x元,则:
(15+x-6)(50-10x)=480,
解得:x1=-1,x2=-3,故没有符合题意的答案;
设售价应降价y元,则:
(15-y-6)(50+10y)=480,
解得:y1=1,y2=3,
由要尽可能的让利给顾客,y=1舍去,则售价为:15-3=12(元),
答:售价应定价为12元;
(2)设单价涨价x元时,每天的利润为w1元,则:
w1=(15+x-6)(50-10x)=-10x2-40x+450
=-10(x+2)2+850,
此时不合题意舍去;
设单价降价y元时,每天的利润为w2元,则:
w2=(15-y-6)(50+10y)
=-10y2+40y+450
=-10(y-2)2+850,
即定价为:15-2=13(元)时,专卖店可以获得最大利润850元.
综上所述:专卖店将单价定为每个13元时,可以获得最大利润850元.
点评 本题考查二次函数与一元二次方程的实际应用,利用数学知识解决实际问题,解题的关键是建立函数模型,利用配方法求最值.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
19.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{18}$ | C. | $\root{3}{2}$ | D. | $\sqrt{20}$ |
1.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a4÷a4=0 | C. | (-2x)3=-6x3 | D. | (a3)4=a12 |
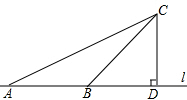 如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732)
如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732) 将两个直角三角形按图中方式叠放,则角α的度数等于75°.
将两个直角三角形按图中方式叠放,则角α的度数等于75°. 阅读下面的证明过程,在括号内补充推理的依据.
阅读下面的证明过程,在括号内补充推理的依据. 如图,在?ABCD中,对角线AC的垂直平分线交BC于E,交AD于F,求证:四边形AECF的菱形.
如图,在?ABCD中,对角线AC的垂直平分线交BC于E,交AD于F,求证:四边形AECF的菱形.