题目内容
3. 阅读下面的证明过程,在括号内补充推理的依据.
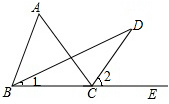
阅读下面的证明过程,在括号内补充推理的依据.已知:如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE.
求证:$\frac{1}{2}$∠A=∠D
证明:∵BD平分∠ABC(已知)
∴∠1=$\frac{1}{2}$∠ABC(角平分线的定义)
同理得∠2=$\frac{1}{2}$∠ACE
又∵∠ACE=∠A+∠ABC(三角形外角的性质)
∴$\frac{1}{2}$∠ACE=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC(等式的性质)
即∠2=$\frac{1}{2}$∠A+∠1(等量代换)
又∵∠2=∠D+∠1
∴$\frac{1}{2}$∠A+∠1=∠D+∠1(三角形外角的性质)
∴$\frac{1}{2}$∠A=∠D.
分析 先根据角平分线的定义得出∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACE,再由三角形外角的性质得出∠ACE=∠A+∠ABC,∠2=∠D+∠1,进而可得出结论.
解答 解:证明:∵BD平分∠ABC(已知),
∴∠1=$\frac{1}{2}$∠ABC(角平分线的定义),
同理得∠2=$\frac{1}{2}$∠ACE.
又∵∠ACE=∠A+∠ABC(三角形外角的性质),
∴$\frac{1}{2}$∠ACE=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC(等式的性质),
即∠2=$\frac{1}{2}$∠A+∠1(等量代换).
又∵∠2=∠D+∠1,
∴$\frac{1}{2}$∠A+∠1=∠D+∠1(三角形外角的性质),
∴$\frac{1}{2}$∠A=∠D.
故答案为:已知,角平分线的定义,三角形外角的性质,等量代换,三角形外角的性质.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.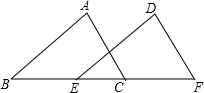 如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
 如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )| A. | AB∥DE,∠A=∠D,BE=CF | B. | AB∥DE,AB=DE,AC=DF | ||
| C. | AB∥DE,AC=DF,BE=CF | D. | AB∥DE,AC∥DF,∠A=∠D |
 如图:E是平行四边形AD边上的一点,连接CE,并延长CE与BA的延长线交于点F,已知CE=ED,∠F=80°,求平行四边形各内角大小.
如图:E是平行四边形AD边上的一点,连接CE,并延长CE与BA的延长线交于点F,已知CE=ED,∠F=80°,求平行四边形各内角大小. 由一个英文单词由五个字母组成,分别对应如图中的有序数对,顺次为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来并翻译成中文为study,“学习”.
由一个英文单词由五个字母组成,分别对应如图中的有序数对,顺次为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来并翻译成中文为study,“学习”.
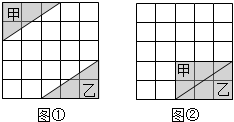 如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么正确的平移方法是向右平移2个格,再向下平移3个格.
如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么正确的平移方法是向右平移2个格,再向下平移3个格.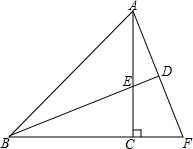 如图,已知等腰直角三角形ABC中,CA=CB,BE平分∠ABC且交AC边于点E,点F在BC的延长线上,∠CAF=∠CBE,延长BE交AF于点D.
如图,已知等腰直角三角形ABC中,CA=CB,BE平分∠ABC且交AC边于点E,点F在BC的延长线上,∠CAF=∠CBE,延长BE交AF于点D.