题目内容
5.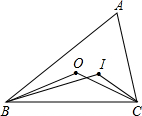 如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )
如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )| A. | ∠BIC=∠BOC | B. | ∠BIC≠∠BOC | ||
| C. | 2∠BIC-$\frac{1}{2}$∠BOC=180° | D. | 2∠BOC-$\frac{1}{2}$∠BIC=180° |
分析 用三角形外心的性质以及圆周角定理得出∠A的度数,进而利用内心的知识得出∠IBC+∠ICB的度数,即可得出答案.
解答 解:∵点O是△ABC的外心,
∴∠A=$\frac{1}{2}$∠BOC,
∵点I是△ABC的内心,
∴∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠BAC),
∴∠BIC=180°-$\frac{1}{2}$(180°-∠BAC)=90°+$\frac{1}{2}$∠A,
∴∠BIC=90°$+\frac{1}{4}$∠BOC,
∴2∠BIC-$\frac{1}{2}$∠BOC=180°;
故选C.
点评 此题主要考查了三角形内心和外心的综合应用,根据题意得出∠IBC+∠ICB的度数是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
14. 如图,已知一次函数y=kx+b的图象,当x<0,y的取值范围是( )
如图,已知一次函数y=kx+b的图象,当x<0,y的取值范围是( )
 如图,已知一次函数y=kx+b的图象,当x<0,y的取值范围是( )
如图,已知一次函数y=kx+b的图象,当x<0,y的取值范围是( )| A. | y>0 | B. | y<0 | C. | y<-2 | D. | 2<y<0 |
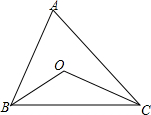 O是△ABC内一点,且BO,CO分别平分∠ABC,∠ACB.
O是△ABC内一点,且BO,CO分别平分∠ABC,∠ACB.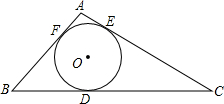 已知:如图,⊙O是△ABC的内切圆,分别切BC、AB、AC于点D、E、F,△ABC的周长为24cm,BC=10cm,则AE=2cm.
已知:如图,⊙O是△ABC的内切圆,分别切BC、AB、AC于点D、E、F,△ABC的周长为24cm,BC=10cm,则AE=2cm.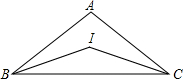 如图,△ABC中,AB=AC,∠ABC=40°,点I是△ABC的内心,则∠BAC的度数为100°.
如图,△ABC中,AB=AC,∠ABC=40°,点I是△ABC的内心,则∠BAC的度数为100°.