题目内容
11.对于方程m2+2(1+$\frac{2}{m}$)=0,用一般的方法去分母将是一个一元三次方程,且好像没有整数解.请你考虑可以采取什么特殊方法找到它的解的范围,要求这个范围在相邻的两个整数之间,并写出这两个整数.分析 根据等式的性质,可化简方程,根据函数与方程的关系,可得答案.
解答 解:由等式的性质,得
m2+2=-$\frac{4}{m}$.
在同一平面直角坐标系内画出n=m2+2,n=-$\frac{4}{m}$, ,
,
由图象,得
n=m2+2与n=-$\frac{4}{m}$的交点坐标在-2与-1之间,
即方程m2+2(1+$\frac{2}{m}$)=0的解在-2与-1之间.
点评 本题考查了函数图象,利用等式的性质把方程转化成m2+2=-$\frac{4}{m}$,利用函数与方程的关系是解题关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
5.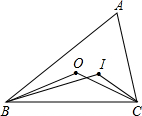 如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )
如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )
 如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )
如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )| A. | ∠BIC=∠BOC | B. | ∠BIC≠∠BOC | ||
| C. | 2∠BIC-$\frac{1}{2}$∠BOC=180° | D. | 2∠BOC-$\frac{1}{2}$∠BIC=180° |
6.函数y=kx+b(k≠0)中,当x的值增加2时,y的值减小3,则k的值为( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | -2 | D. | -3 |
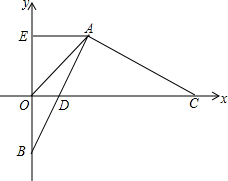 已知如图,AE∥x轴,OA平分∠EOC,点A(2,2),点B(0,-2),AB交x轴于点D,AC⊥AB交x轴于点C,且AB=AC.
已知如图,AE∥x轴,OA平分∠EOC,点A(2,2),点B(0,-2),AB交x轴于点D,AC⊥AB交x轴于点C,且AB=AC.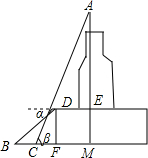 如图所示为某大厦的示意图其中裙楼共有10层,现测得DF的高为55米,吴莉在D处测得地面上点B的俯角α为30°,点D到AM的距离DE为60米,从地面上的点B沿BM方向走到点C处,测得BC=50米,大厦顶尖A的仰角β为65°,请根据以上测量数据计算大厦的高AM.(结果精确到0.1米,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.143,$\sqrt{3}$≈1.732)
如图所示为某大厦的示意图其中裙楼共有10层,现测得DF的高为55米,吴莉在D处测得地面上点B的俯角α为30°,点D到AM的距离DE为60米,从地面上的点B沿BM方向走到点C处,测得BC=50米,大厦顶尖A的仰角β为65°,请根据以上测量数据计算大厦的高AM.(结果精确到0.1米,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.143,$\sqrt{3}$≈1.732) 如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E.
如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E.