题目内容
20.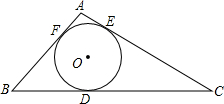 已知:如图,⊙O是△ABC的内切圆,分别切BC、AB、AC于点D、E、F,△ABC的周长为24cm,BC=10cm,则AE=2cm.
已知:如图,⊙O是△ABC的内切圆,分别切BC、AB、AC于点D、E、F,△ABC的周长为24cm,BC=10cm,则AE=2cm.
分析 由切线长定理,可知:AE=AF,CD=CE,BF=BD,设AF=AE=x;BD=BF=y;CE=CD=z,利用已知数据建立方程组即可求出AE的长.
解答 解:∵⊙O是△ABC的内切圆,分别切BC、AB、AC于点D、E、F,
设AF=AE=x;BD=BF=y;CE=CD=z,
根据题意得:$\left\{\begin{array}{l}{2x+2y+2z=24}\\{y+z=10}\end{array}\right.$,
解得x=2,
∴AE=2.
点评 此题主要是考查了切线长定理,用已知数和未知数表示所有的切线长,再进一步列方程组求解.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
5.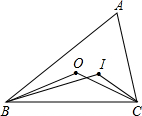 如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )
如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )
 如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )
如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )| A. | ∠BIC=∠BOC | B. | ∠BIC≠∠BOC | ||
| C. | 2∠BIC-$\frac{1}{2}$∠BOC=180° | D. | 2∠BOC-$\frac{1}{2}$∠BIC=180° |
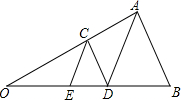 已知,如图,在△AOB中,点C在OA上,点E、D在OB上,且AB=AD,CD∥AB,CE∥AD,问:△CDE是否为等腰三角形?为什么?
已知,如图,在△AOB中,点C在OA上,点E、D在OB上,且AB=AD,CD∥AB,CE∥AD,问:△CDE是否为等腰三角形?为什么?
 如图,⊙O与△ABC各边切于点D、E、F,且∠C=60°,∠EOF=100°,求∠B的度数.
如图,⊙O与△ABC各边切于点D、E、F,且∠C=60°,∠EOF=100°,求∠B的度数.