题目内容
10．
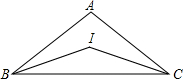如图，△ABC中，AB=AC，∠ABC=40°，点I是△ABC的内心，则∠BAC的度数为100°．
分析 根据等腰三角形的性质得到∠ACB=∠ABC=40°，再由内心的定义即可求得∠IBC+∠ICB，然后根据三角形内角和定理即可求解．
解答 解：∵AB=AC，∠ACB=∠ABC=40°，
∵点I是△ABC的内心，
∴∠IBC=$\frac{1}{2}$∠ABC=20°，∠ICB=$\frac{1}{2}$∠ACB=20°，
∴∠IBC+∠ICB=40°，
∴∠BIC=180°-（∠IBC+∠ICB）=140°．
∴∠BAC=180°-（∠ABC+∠ACB）=100°．
点评 此题主要考查了三角形的内心的计算，正确理解∠IBC=$\frac{1}{2}$∠ABC=20°，∠ICB=$\frac{1}{2}$∠ACB=20°是关键．
练习册系列答案
相关题目
如图，I是△ABC的内心，∠BAC的平分线与△ABC的外接圆相交于点D，交BC于点E．
18．已知三角形三边长分别为5cm、5cm、6cm，则这个三角形内切圆的半径是（ ）
| A． | $\frac{9}{8}$cm | B． | $\frac{3}{2}$cm | C． | 2cm | D． | 3cm |
5．
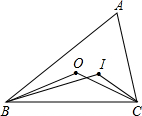如图，点I和O分别是△ABC的内心和外心，则∠BIC与∠BOC的关系为（ ）
如图，点I和O分别是△ABC的内心和外心，则∠BIC与∠BOC的关系为（ ）| A． | ∠BIC=∠BOC | B． | ∠BIC≠∠BOC | ||
| C． | 2∠BIC-$\frac{1}{2}$∠BOC=180° | D． | 2∠BOC-$\frac{1}{2}$∠BIC=180° |
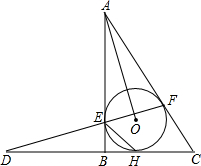已知：如图，Rt△ABC外切于圆O，切点分别为E、F、H，∠ABC=90°，直线FE、CB交于D点，连接AO、HE．现给出以下四个结论：①∠FEH=90°-$\frac{1}{2}$∠C；②DE=AE；③AB2=AO•DF；④AE•CH=S△ABC，其中正确结论的序号为①③④．
2．下面计算结果正确的是（ ）
| A． | （-3）0=1 | B． | a3+a3=a6 | C． | 4m-4=$\frac{1}{{4{m^4}}}$ | D． | （xy2）3=xy6 |
19．如果a的倒数是-2，那么a等于（ ）
| A． | 2 | B． | -2 | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |