题目内容
3. 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
分析 (1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB=$\sqrt{3}$,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,
∵DE⊥AF,
∴∠AED=90°=∠B,
在△ABF和△DEA中
$\left\{\begin{array}{l}{∠AFB=∠DAE}\\{∠B=∠DEA}\\{AF=AD}\end{array}\right.$,
∴△ABF≌△DEA(AAS),
∴DE=AB;
(2)解:∵BC=AD,AD=AF,
∴BC=AF,
∵BF=1,∠ABF=90°,
∴由勾股定理得:AB=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴∠BAF=30°,
∴扇形ABG的面积=$\frac{30π×(\sqrt{3})^{2}}{360}$=$\frac{π}{4}$.
点评 本题考查了弧长公式,全等三角形的性质和判定,解直角三角形,勾股定理,矩形的性质的应用,能综合运用性质进行推理和计算是解此题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
18. 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )| A. | 16 | B. | 24 | C. | 32 | D. | 48 |
15. 如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
 如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )| A. | △ACD的外心 | B. | △ABC的外心 | C. | △ACD的内心 | D. | △ABC的内心 |
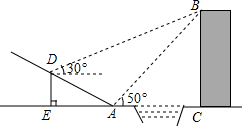 如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数) 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
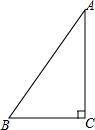 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.