题目内容
已知关于x的一元二次方程x2-3x-k=0有两个不相等的实数根.
(1)求k的取值范围.
(2)求k的负整数值,并选择一个k的负整数值,求出方程的根.
(1)求k的取值范围.
(2)求k的负整数值,并选择一个k的负整数值,求出方程的根.
考点:根的判别式
专题:
分析:(1)根据判别式的意义得到△=(-3)2+4k>0,然后解不等式即可;
(2)选取一个k的负整数值,求出方程的根即可.
(2)选取一个k的负整数值,求出方程的根即可.
解答:解:(1)∵关于x的一元二次方程x2-3x-k=0有两个不相等的实数根,
∴△=(-3)2+4k>0,
解得:k>-
;
(2)假设k=-2,
则x2-3x+2=0,
解得:x1=1,x2=2,.
∴△=(-3)2+4k>0,
解得:k>-
| 9 |
| 4 |
(2)假设k=-2,
则x2-3x+2=0,
解得:x1=1,x2=2,.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
将二次函数y=2x2向左平移3个单位,再向下平移5个单位,则得到新的图象的二次函数表达式是( )
| A、y=2(x-3)2-5 |
| B、y=2(x+3)2-5 |
| C、y=2(x+3)2+5 |
| D、y=2(x-3)2+5 |
二次函数y=ax2+bx+c的部分对应值如表:
下面关于二次函数及其图象说法不正确的是( )
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |
| A、对称轴为x=1 |
| B、y的最大值是-9 |
| C、x=2对应的函数值y=-8 |
| D、抛物线截x轴所得的线段长是6 |
下列命题为真命题的是( )
| A、若直线y=-kx+2过二、四象限,则k>0 |
| B、有两边和一角分别相等的两个三角形全等 |
| C、直线y=2x-3在y轴上的截距为3 |
| D、△ABC中,若∠A=2∠B=3∠C,那么△ABC为直角三角形 |
已知二次函数y=a(x+m)2+m(a≠0),无论m为何实数其图象的顶点都在( )
| A、x轴上 | B、y轴上 |
| C、直线y=x上 | D、直线y=-x上 |
 如图,A、B是函数y=
如图,A、B是函数y=| 2 |
| x |
| A、S=2 | B、S=4 |
| C、S=8 | D、S=1 |
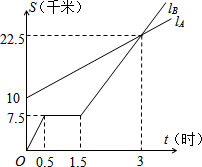 如图,lA与 lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.B自行车遇到故障中途停下修理1小时.若B的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与A相遇?
如图,lA与 lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.B自行车遇到故障中途停下修理1小时.若B的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与A相遇?