题目内容
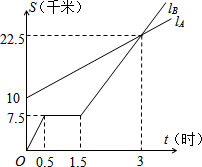 如图,lA与 lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.B自行车遇到故障中途停下修理1小时.若B的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与A相遇?
如图,lA与 lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.B自行车遇到故障中途停下修理1小时.若B的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与A相遇?考点:一次函数的应用
专题:
分析:根据题意分别得出lA与 lB的解析式,进而求出相遇时的时间.
解答:解:设lB的解析式为:lB=kt,
则7.5=0.5k,
解得:k=15,
故lB=15t;
设lA的解析式为:lA=at+b,
则
,
解得:
,
故lA=
t+10,
当lA=lB,
则
t+10=15t,
解得:t=
,
即经过
小时与A相遇.
则7.5=0.5k,
解得:k=15,
故lB=15t;
设lA的解析式为:lA=at+b,
则
|
解得:
|
故lA=
| 25 |
| 6 |
当lA=lB,
则
| 25 |
| 6 |
解得:t=
| 12 |
| 13 |
即经过
| 12 |
| 13 |
点评:此题主要考查了一次函数的应用,根据题中已知图象得出点的坐标求出解析式是解题关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
在同一直角坐标系中,函数y=bx-a和y=ax-b的图象可能是( )
A、 |
B、 |
C、 |
D、 |
 如图,平放的圆柱的主视图、左视图、俯视图分别是( )
如图,平放的圆柱的主视图、左视图、俯视图分别是( )| A、圆、长方形、圆 |
| B、长方形、圆、圆 |
| C、长方形、圆、长方形 |
| D、长方形、长方形、圆 |
 点P在第一象限,坐标为(m,n).
点P在第一象限,坐标为(m,n).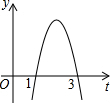 二次函数y=ax2+bx+c的图象如图所示,以下结论:①a+b+c=0;②4a+b=0;③abc<0;④4ac-b2<0,其中正确的有( )个.
二次函数y=ax2+bx+c的图象如图所示,以下结论:①a+b+c=0;②4a+b=0;③abc<0;④4ac-b2<0,其中正确的有( )个.