题目内容
5.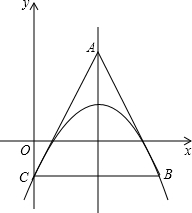 如图,抛物线y=a(x-2)2+k与y轴交于点C,过点C作CB∥x轴,与抛物线交于点B,若点A是其对称轴上的一点,且∠ACB=60°,连接AB,则S△ABC的值为4$\sqrt{3}$.
如图,抛物线y=a(x-2)2+k与y轴交于点C,过点C作CB∥x轴,与抛物线交于点B,若点A是其对称轴上的一点,且∠ACB=60°,连接AB,则S△ABC的值为4$\sqrt{3}$.
分析 根据抛物线的对称性求得BC=4,解直角三角形求得AD=2$\sqrt{3}$,然后根据三角形面积公式即可求得.
解答 解:∵AD是抛物线y=a(x-2)2+k的对称轴,
∴AD⊥x轴,
∵CB∥x轴,
∴AD⊥CB,
∵CD=BD,
∴AC=AB,
∵∠ACB=60°,
∴△ABC是等边三角形,
∵对称轴x=2,
∴CD=2,
∴BC=2CD=4,AD=CD•tag60°=2×$\sqrt{3}$=2$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$,
故答案为4$\sqrt{3}$.
点评 本题考查了二次函数的性质,等边三角形的面积,根据抛物线的对称性得出等边三角形的边长是解题的关键.

练习册系列答案
相关题目
9.最薄的金箔的厚度为0.000000091m,0.000000091这个数学科学记数法表示正确的是( )
| A. | 9.1×10-8 | B. | 9.1×10-7 | C. | 0.91×10-8 | D. | 0.91×10-7 |
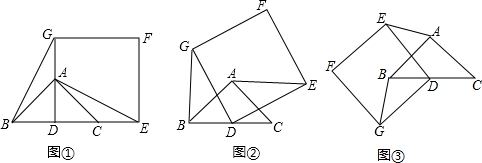
14.下列能判定四边形是平行四边形的有( )
| A. | 一组对边相等,一组对角也相等 | |
| B. | 一组对边相等,一条对角线被另一条平分 | |
| C. | 一组对角相等,一条对角线被另一条平分 | |
| D. | 一组对角相等,过这组对角的顶点的对角线平分另一条对角线 |
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.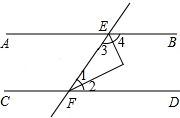 如图,直线AB,CD被EF所截,∠1=∠2,∠3=∠4,∠1+∠3=90°,那么AB与CD平行吗?为什么?
如图,直线AB,CD被EF所截,∠1=∠2,∠3=∠4,∠1+∠3=90°,那么AB与CD平行吗?为什么?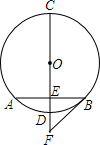 如图,CD是⊙O的直径,弦AB⊥CD于点E,且AB=2$\sqrt{2}$,DE=2-$\sqrt{2}$.
如图,CD是⊙O的直径,弦AB⊥CD于点E,且AB=2$\sqrt{2}$,DE=2-$\sqrt{2}$.