��Ŀ����
17��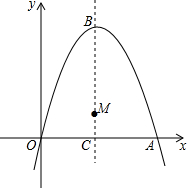 ��ͼ������ԭ���������y=-x2+2mx��m��0����x�����һ������Ϊ��A������Ϊ��B�������ߵĶԳ�����x�ύ�ڵ�C����M�������ߵĶԳ����ϣ���������Ϊ1��
��ͼ������ԭ���������y=-x2+2mx��m��0����x�����һ������Ϊ��A������Ϊ��B�������ߵĶԳ�����x�ύ�ڵ�C����M�������ߵĶԳ����ϣ���������Ϊ1����1����m=2ʱ��
�ٵ�A������Ϊ��4��0������B������Ϊ��2��4��B����M������Ϊ��2��1����
�ڹ���M��MN��AB����x���ڵ�N�����MCN�������
��2����BC=2BMʱ����ֱ��д��m��ֵ��
��3����m=$\sqrt{5}$����P��Q�ֱ�ӵ�O�͵�Aͬʱ����������ͬ���ٶ����C�˶�����P��Q�����Cʱ��ֹͣ�˶�������BP��BQ��MP��MQ������PMQ=3��PBQʱ����ֱ��д����PBQ�������ֵ��
���� ��1����һԪ���η���-x��x-4��=0�������䷽��ȷ���������꼴�ɣ�
��2�����ô���ϵ����ȷ����ֱ��AB�Ľ���ʽΪy=-2x+8������ƽ����ͨ����Mȷ����ֱ��MN�Ľ���ʽ���Ӷ����CN���ɣ�
��3�����PC�����PB=$\sqrt{{a}^{2}+25}$PM=$\sqrt{{a}^{2}+1}$��BR=$\frac{1}{2}$PB=$\frac{1}{2}$$\sqrt{{a}^{2}+25}$�����á�BRN�ס�BCP����ʾ��BN�������ó�MN������ý�ƽ���߶����������̼��ɣ�
��� �⣺��1���١�m=2��
��y=-x2+4x=-x��x-4��=0��
��x1=0��x2=4��
��A��4��0����
��y=-x2+4x=-��x-2��2+4��
��B��2��4����
�ߵ�M�������ߵĶԳ����ϣ���������Ϊ1��
��M��2��1����
�ʴ�ΪA��4��0����B��2��4����M��2��1����
����ͼ1��
��ֱ��AB�Ľ���ʽΪy=kx+b��
����������$\left\{\begin{array}{l}{4k+b=0}\\{2k+b=4}\end{array}\right.$��
��$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy=-2x+8��
��MN��AB���ҹ���M��2��1��
��ֱ��MN�Ľ���ʽΪy=-2x+5��
��N��x���ϣ�
��N��$\frac{5}{2}$��0����
��C��2��0��
��CN=$\frac{1}{2}$��
��CM=1��
��S��MCN=$\frac{1}{2}$��CN��CM=$\frac{1}{2}$��$\frac{1}{2}$��1=$\frac{1}{4}$��
��2����������y=-x2+2mx=-x��x-2m����
��A��2m��0����
��������y=-x2+2mx=-��x-m��2+m2��
��B��m��m2����C��m��0����
�ߵ�M�������ߵĶԳ����ϣ���������Ϊ1��
��M��m��1����
��BC=m2��BM=|m2-1|��
��BC=2BM��
��m2=2|m2-1|��
��m1=$\sqrt{2}$��m2=-$\sqrt{2}$���ᣩ��m3=$\frac{\sqrt{6}}{3}$��m4=-$\frac{\sqrt{6}}{3}$���ᣩ��
��m1=$\sqrt{2}$��m2=$\frac{\sqrt{6}}{3}$��
��3����ͼ2��
��m=$\sqrt{5}$��
��������y=-x2+2mx=-��x-m��2+m2=-��x-$\sqrt{5}$��2+5��
��B��$\sqrt{5}$��5����C��$\sqrt{5}$��0��
��BC=5��MC=1��BM=4��
����BPM��ƽ���߽�BC��N������N��NR��AB��
�ߡ�PMQ=3��PBQ��
���BPN=��MPN=��PBC��
��PC=a��
��PB=$\sqrt{{a}^{2}+25}$PM=$\sqrt{{a}^{2}+1}$��
��BR=$\frac{1}{2}$PB=$\frac{1}{2}$$\sqrt{{a}^{2}+25}$
�ߡ�RBN=��CBP����BRN=��BCP��
���BRN�ס�BCP��
��$\frac{BN}{PB}=\frac{BR}{BC}$��
��$\frac{BN}{\sqrt{{a}^{2}+25}}=\frac{\frac{1}{2}\sqrt{{a}^{2}+25}}{5}$
��BN=$\frac{{a}^{2}+25}{10}$��
��MN=BM-BN=$\frac{15-{a}^{2}}{10}$��
��PN�ǡ�BPM�Ľ�ƽ���ߣ�
��$\frac{BN}{MN}=\frac{PB}{PM}$��
��$\frac{\frac{{a}^{2}+25}{10}}{\frac{15-{a}^{2}}{10}}=\frac{\sqrt{{a}^{2}+25}}{\sqrt{{a}^{2}+1}}$��
��a=-$\frac{5\sqrt{7}}{7}$���ᣩ��a=$\frac{5\sqrt{7}}{7}$
��PQ=$\frac{10\sqrt{7}}{7}$��
��S��PBQ=$\frac{1}{2}$��PQ��BC=$\frac{1}{2}$��$\frac{10\sqrt{7}}{7}$��5=$\frac{25\sqrt{7}}{7}$
������PBQ�����Ϊ=$\frac{25\sqrt{7}}{7}$��
���� ������κ����ۺ��⣬��Ҫ�������ô���ϵ������ֱ�߽���ʽ��ȷ���������꣬�����ε��������ƽ���߶������Ȿ��Ĺؼ���Ҫ����ȷ����������x��Ľ�������Ͷ������꣮�����������ǽⱾ����ѵ㣮

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�| A�� | 901��999 | B�� | 922��978 | C�� | 950��950 | D�� | 961��939 |
 ��ͼ1���ֻ������ֻ�֧���ϣ������ʾ��ͼ��ͼ2��ʾ��AB��CD�dz��Ȳ���ĻƬ��һ��A�̶���0A�ϣ���һ��B����0C�ϱ䶯λ�ã�����AB�䵽AB���λ�ã���0C��תһ���Ƕȵ���0C���λ�ã���֪0A=8cm��AB��0C����B0A=60�㣬sin��B��A0=$\frac{9}{10}$�����B�䵽0A�ľ���Ϊ��������
��ͼ1���ֻ������ֻ�֧���ϣ������ʾ��ͼ��ͼ2��ʾ��AB��CD�dz��Ȳ���ĻƬ��һ��A�̶���0A�ϣ���һ��B����0C�ϱ䶯λ�ã�����AB�䵽AB���λ�ã���0C��תһ���Ƕȵ���0C���λ�ã���֪0A=8cm��AB��0C����B0A=60�㣬sin��B��A0=$\frac{9}{10}$�����B�䵽0A�ľ���Ϊ��������| A�� | $\frac{9\sqrt{3}}{10}$cm | B�� | $\frac{18\sqrt{3}}{10}$cm | C�� | $\frac{9\sqrt{3}}{5}$cm | D�� | $\frac{18\sqrt{3}}{5}$cm |
| A�� | y��0 | B�� | -3��y��-1 | C�� | -6��y��-2 | D�� | 2��y��6 |
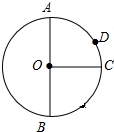 AB�ǡ�O��ֱ������AB=2��OC��AB������Ϊ��O����AD����DC=2��1����OC����һ����P����PA+PD����СֵΪ$\sqrt{3}$��
AB�ǡ�O��ֱ������AB=2��OC��AB������Ϊ��O����AD����DC=2��1����OC����һ����P����PA+PD����СֵΪ$\sqrt{3}$��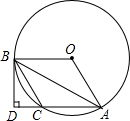 ��ͼ��AB�ǡ�O���ң���O����AB�ĶԳƵ�C�ڡ�O�ϣ�����B��BD��AC��AC���ӳ����ڵ�D��
��ͼ��AB�ǡ�O���ң���O����AB�ĶԳƵ�C�ڡ�O�ϣ�����B��BD��AC��AC���ӳ����ڵ�D��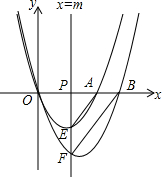 ��ͼ����ֱ��x=m��m��0���ֱ�x�ᣬ������y=x2-3x��y=x2-4x�ڵ�P��E��F�����A��BΪ������y=x2-3x��y=x2-4x��x���һ�����㣬����AE��BF��
��ͼ����ֱ��x=m��m��0���ֱ�x�ᣬ������y=x2-3x��y=x2-4x�ڵ�P��E��F�����A��BΪ������y=x2-3x��y=x2-4x��x���һ�����㣬����AE��BF��