题目内容
5.2010-2|1-x|-|4+2x|-x2的最大值是2004.分析 分四种情况:①x≤-2,②-2<x≤0,③0<x≤1,④x>1,进行讨论可求2010-2|1-x|-|4+2x|-x2的最大值.
解答 解:①x≤-2,
2010-2|1-x|-|4+2x|-x2
=2010-2+2x+4+2x-x2
=-(x-2)2+2016,
最大值是2000;
②-2<x≤0,
2010-2|1-x|-|4+2x|-x2
=2010-2+2x-4-2x-x2
=-x2+2004,
最大值是2004;
③0<x≤1,
2010-2|1-x|-|4+2x|-x2
=2010-2+2x-4-2x-x2
=-x2+2004,
最大值小于2004;
④x>1,
2010-2|1-x|-|4+2x|-x2
=2010+2-2x-4-2x-x2
=-(x+2)2+2008,
最大值小于1999;
综上所述,2010-2|1-x|-|4+2x|-x2的最大值是2004.
故答案为:2004.
点评 考查了绝对值,当a是正有理数时,a的绝对值是它本身a; ②当a是负有理数时,a的绝对值是它的相反数-a; ③当a是零时,a的绝对值是零.关键是分类思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.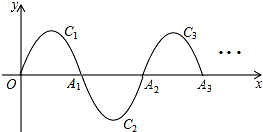 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )
 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )| A. | 2 | B. | -2 | C. | 0 | D. | $\frac{9}{4}$ |
13. 如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
 如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )| A. | (6$\sqrt{3}$-$\frac{4}{3}$π)m2 | B. | (8$\sqrt{3}$-$\frac{4}{3}$π)m2 | C. | (6$\sqrt{3}$-$\frac{8}{3}$π)m2 | D. | (8$\sqrt{3}$-$\frac{8}{3}$π)m2 |
15.-5的绝对值是( )
| A. | 5 | B. | -$\frac{1}{5}$ | C. | -5 | D. | $\frac{1}{5}$ |
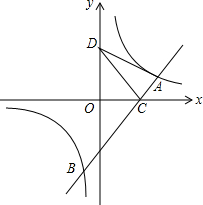 如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC.
如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC. 如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50.
如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50.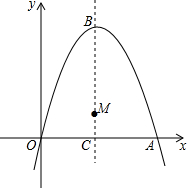 如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为点A,顶点为点B.抛物线的对称轴与x轴交于点C,点M在抛物线的对称轴上,且纵坐标为1.
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为点A,顶点为点B.抛物线的对称轴与x轴交于点C,点M在抛物线的对称轴上,且纵坐标为1. 如图所示的图案绕点O顺时针旋转,至少旋转120°后,与原来的图案重合.
如图所示的图案绕点O顺时针旋转,至少旋转120°后,与原来的图案重合.