题目内容
2.解不等式:(组),并把解集表示在数轴上.(1)$\frac{x+2}{4}$-$\frac{2x-3}{6}$≥1
(2)$\left\{\begin{array}{l}{2x-7<3(1-x)}\\{\frac{4}{3}x+3≥1-\frac{2}{3}x}\end{array}\right.$.
分析 (1)首先去分母,然后去括号、移项、合并同类项、系数化成1即可求解;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组组的解集.
解答 解:(1)去分母3(x+2)-2(2x-3)≥12,
去括号3x+6-4x+6≥12,
移项得x≤0;
(2)$\left\{\begin{array}{l}{2x-7<3(1-x)…①}\\{\frac{4}{3}x+3≥1-\frac{2}{3}x…②}\end{array}\right.$,
解①得x<2,
解②得x≥-1.
则不等式组的解集是:-1≤x<2.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
7.若x2-2x-5=0的一个解为a,则a(2a-3)+a(1-a)的值为( )
| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$+4 | C. | 5 | D. | -5 |
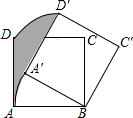 如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.
如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.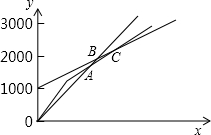 2015年12月19日郑州机场T2航站楼正式启用,为了宣传T2航站楼,机场反面要印刷一批宣传材料,经招标,某印务公司中标,该印务公司提出3种方案:
2015年12月19日郑州机场T2航站楼正式启用,为了宣传T2航站楼,机场反面要印刷一批宣传材料,经招标,某印务公司中标,该印务公司提出3种方案: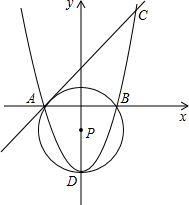 在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).
在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).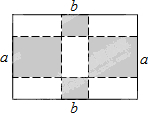 如图,将一张长方形大铁皮切割(切痕为虚线)成九块,其中有两块是边长都为a厘米的大正方形,两块是边长都为b厘米的小正方形,且a>b.
如图,将一张长方形大铁皮切割(切痕为虚线)成九块,其中有两块是边长都为a厘米的大正方形,两块是边长都为b厘米的小正方形,且a>b.