题目内容
8．
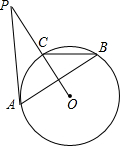如图，PA与⊙O相切于点A，PO交⊙O于点C，点B是优弧CBA上一点，若∠P=26°，则∠ABC的度数为（ ）| A． | 26° | B． | 64° | C． | 32° | D． | 90° |
分析 连接OA，则△PAO是直角三角形，根据根据直角三角形的性质∠POA的度数，进而根据圆周角定理即可求解．
解答 
解：连接OA．
∴∠PAO=90°，
∵∠O=90°-∠P=64°，
∴∠B=$\frac{1}{2}$∠O=32°．
故选C．
点评 本题主要考查了切线的性质，以及圆周角定理，正确利用定理，作出辅助线求得∠POA的度数是解题的关键．
练习册系列答案
相关题目
18．对于实数a、b，定义一种运算“?”为：a?b=a2+ab-2，有下列命题：
①1?3=2；②方程x?1=0的根为：x1=-2，x2=1；③不等式组$\left\{\begin{array}{l}{（-2）?x-4＜0}\\{1?x-3＜0}\end{array}\right.$的解集为：-1＜x＜4；④点（1，-2）在函数y=x?（-1）的图象上．
其中正确的是（ ）
①1?3=2；②方程x?1=0的根为：x1=-2，x2=1；③不等式组$\left\{\begin{array}{l}{（-2）?x-4＜0}\\{1?x-3＜0}\end{array}\right.$的解集为：-1＜x＜4；④点（1，-2）在函数y=x?（-1）的图象上．
其中正确的是（ ）
| A． | ①②③④ | B． | ①③④ | C． | ①②④ | D． | ①②③ |
19．气温由-2℃上升3℃后是（ ）
| A． | -5℃ | B． | 1℃ | C． | 5℃ | D． | 3℃ |
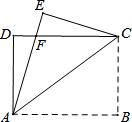如图，矩形ABCD中，AB=8，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F，若AF=$\frac{25}{4}$，则AD的长为（ ）
20．下列函数的图象中，有最低点的函数是（ ）
| A． | y=-4x2 | B． | y=-2x+3 | C． | y=3x+5 | D． | y=$\frac{1}{4}$x2 |