题目内容
身高相同的三个小朋友甲、乙、丙放风筝，他们放出的线长分别为300m，250 m，200m；线与地面所成的角度分别为30°，45°，60°(假设风筝线是拉直的)，则三人所放的风筝（ ）
A．甲的最高 B．乙的最低 C．丙的最低 D．乙的最高
D．
【解析】
试题解析：甲放的高度为：300×sin30°=150米．
乙放的高度为：250×sin45°=125≈176.75米．
丙放的高度为：200×sin60°=100≈173.2米．
所以乙的最高．
故选D．
如图，某校的围墙由一段相同的凹曲拱组成，其拱状图形为抛物线的一部分，栅栏的跨径AB间，按相同间隔0.2米用5根立柱加固，拱高OC为0.36米，则立柱EF的长为（ ）
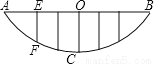
A. 0.4米 B. 0.16米 C. 0.2米 D. 0.24米
C
【解析】如图，以C坐标系的原点，OC所在直线为y轴建立坐标系，
设抛物线解析式为y=ax2，由题知，图象过B（0.6，0.36），代入得：0.36=0.36a
∴a=1，即y=x2．∵F点横坐标为-0.4，∴当x=-0.4时，y=0.16，∴EF=0.36-0.16=0.2米.故选C． 2013年5月26日，中国羽毛球队蝉联苏迪曼杯团体赛冠军，成就了首个五连冠霸业．比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图)，若不考虑外力因素，羽毛球行进高度y(米)与水平距离x(米)之间满足关系y＝－
x2＋
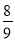x＋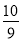
，则羽毛球飞出的水平距离为__________米．
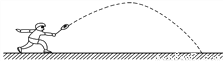
5
【解析】试题解析：当y=0时，0＝，
解得：x1=-1（舍去），x2=5，
故羽毛球飞出的水平距离为5m． 若二次函数y＝x2＋bx＋4配方后为y＝(x－2)2＋k，则b、k的值分别为( )
A. 0，5 B. 0，1 C. －4，5 D. －4，0
D
【解析】∵二次函数y＝x2＋bx＋4配方后是y＝（x－2）2＋k
∴a=1， -=2， c=4
∴b=-4
∴ k==1
故选：D. 如图是石景山当代商场地下广场到地面广场的手扶电梯示意图．其中AB、CD分别表示地下广场、地面广场电梯口处的水平线．已知∠ABC=135°，BC的长约是6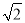
m，则乘电梯从点B到点C上升的高度h是_________．
6m
【解析】试题分析：
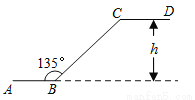
过点C作CM⊥AB交AB的延长线于点M, 由∠ABC=135°可得∠CBM=45°，在Rt△BMC中，由锐角三角函数即可求得CM=6． 如图，某水渠的横断面是等腰梯形，已知其斜坡AD和BC的坡度为1：0.6，现测得放水前的水面宽EF为1.2米，当水闸放水后，水渠内水面宽GH为2.1米．求放水后水面上升的高度是（ ）
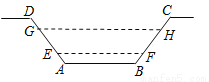
A. 0.55 B. 0.8 C. 0.6 D. 0.75
D
【解析】试题分析：过点E作EM⊥GH，则GM=(2.1-1.2)÷2=0.45米，根据坡度可得：EM=0.45÷0.6=0.75米，故选D． 如图，AC是电线杆AB的一根拉线，测得BC的长为6米，∠ACB=50°，则拉线AC的长为（ ）
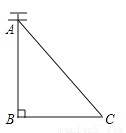
A.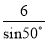 
B.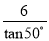 
C. 6cos50° D.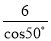 
D
【解析】试题分析：根据Rt△ABC中∠C的余弦值可得：cos50°=，则AC=，故选D． 对于抛物线y＝ax2，下列说法中正确的是（ ）
A. a越大，抛物线开口越大
B. a越小，抛物线开口越大
C. ｜a｜越大，抛物线开口越大
D. ｜a｜越小，抛物线开口越大
D
【解析】试题分析：∵对于y＝ax2图像而言，|a|越小，开口越大
∴D是正确的 如果二次函数的二次项系数为l，则此二次函数可表示为y=x2+px+q，我们称[p，q]为此函数的特征数，如函数y=x2+2x+3的特征数是[2，3]．
（1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．
（2）探究下列问题：
①若一个函数的特征数为[2，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．
②若一个函数的特征数为[4，2]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[2，4]？
（1）此函数图象的顶点坐标为：（1，0）；（2）图象对应的函数的特征数为：[0，﹣1]；（3）原函数的图象向右平移1个单位，再向上平移5个单位得到．
【解析】试题分析：（1）根据特征数的定义，得二次函数为y=x2﹣2x+1，再利用配方得：y=（x﹣1）2，从而顶点坐标为（1,0）
（2）①根据特征数的定义，得二次函数为y=x2+2x-1，再利用配方得y=（x+1）2﹣2，图象先向右平移...