Question

14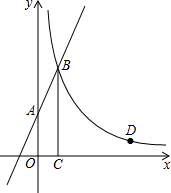．如图，直线y=2x+3与y轴交于A点，与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点B，过点B作BC⊥x轴于点C，且C点的坐标为（1，0）．
（1）求反比例函数的解析式；
（2）点D（a，1）是反比例函数y=$\frac{k}{x}$（x＞0）图象上的点，在x轴上是否存在点P，使得PB+PD最小？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）先根据直线y=2x+3求出点B坐标，再利用待定系数法可求得反比例函数解析式；
（2）先根据反比例函数解析式求出点D 的坐标，若要在x轴上找一点P，使PB+PD最小，可作点D关于x的轴的对称点D′，连接BD′，直线BD′与x轴的交点即为所求点P．

解答 解：（1）∵BC⊥x轴于点C，且C点的坐标为（1，0），
∴在直线y=2x+3中，当x=1时，y=2+3=5，
∴点B的坐标为（1，5），
又∵点B（1，5）在反比例函数y=$\frac{k}{x}$上，
∴k=1×5=5，
∴反比例函数的解析式为：y=$\frac{5}{x}$；
（2）将点D（a，1）代入y=$\frac{5}{x}$，得：a=5，
∴点D坐标为（5，1）
设点D（5，1）关于x轴的对称点为D′（5，-1），
过点B（1，5）、点D′（5，-1）的直线解析式为：y=kx+b，
可得：$\left\{\begin{array}{l}{k+b=5}\\{5k+b=-1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=\frac{13}{2}}\end{array}\right.$，
∴直线BD′的解析式为：y=-$\frac{3}{2}$x+$\frac{13}{2}$，
根据题意知，直线BD′与x轴的交点即为所求点P，
当y=0时，得：-$\frac{3}{2}$x+$\frac{13}{2}$=0，解得：x=$\frac{13}{3}$，
故点P的坐标为（$\frac{13}{3}$，0）．

点评 本题主要考查一次函数与反比例函数的交点问题及依据轴对称性质求最短路线问题，待定系数法求一次函数、反比例函数的解析式是解题关键．