题目内容
5. 如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.
如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.
分析 欲证明AF=DF只要证明△ABF≌△DEF即可解决问题.
解答 证明: ∵AB∥CD,
∵AB∥CD,
∴∠B=∠FED,
在△ABF和△DEF中,
$\left\{\begin{array}{l}{∠B=∠FED}\\{BF=EF}\\{∠AFB=∠EFD}\end{array}\right.$,
∴△ABF≌△DEF,
∴AF=DF.
点评 本题考查全等三角形的判定和性质,平行线的性质等知识,解题的关键是熟练掌握全等三角形的判断和性质,熟练掌握平行线的性质,属于基础题,中考常考题型.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.在2016年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数,方差依次为( )
| 成绩(分) | 27 | 28 | 30 |
| 人数 | 2 | 3 | 1 |
| A. | 28,28,1 | B. | 28,27.5,1 | C. | 3,2.5,5 | D. | 3,2,5 |
20.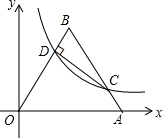 如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
 如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )| A. | 25$\sqrt{3}$ | B. | 18$\sqrt{3}$ | C. | 9$\sqrt{3}$ | D. | 9 |
10. 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )
二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )
 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )
二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.下列各图中,可围成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
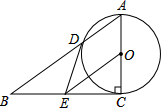 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点O作OE∥AB交BC于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点O作OE∥AB交BC于点E,连接DE. 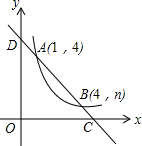 如图,直线y=ax+b与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
如图,直线y=ax+b与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.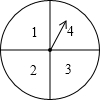 小明和小军两人一起做游戏,游戏规则如下:每人从1,2,…,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于他们各自选择的数,就在做一次上述游戏,直至决出胜负.若小军事先选择的数是5,用列表或画树状图的方法求他获胜的概率.
小明和小军两人一起做游戏,游戏规则如下:每人从1,2,…,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于他们各自选择的数,就在做一次上述游戏,直至决出胜负.若小军事先选择的数是5,用列表或画树状图的方法求他获胜的概率.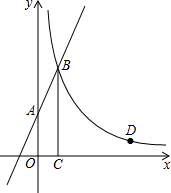 如图,直线y=2x+3与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
如图,直线y=2x+3与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).