题目内容
5. 如图,斜面AC的坡度为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为( )
如图,斜面AC的坡度为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为( )| A. | 5米 | B. | 6米 | C. | 8米 | D. | (3+$\sqrt{5}$)米 |
分析 根据题意可得,在Rt△ACD中,CD:AD=1:2,设CD=x,AD=2x,又AC=3$\sqrt{5}$米,利用勾股定理列方程求出x的值,然后得出AD的长度,在Rt△ABD中求出BD的高度,最后BD-CD即可求出BC的高度.
解答 解:在Rt△ACD中,
∵CD:AD=1:2,
∴设CD=x,AD=2x,
又∵AC=3$\sqrt{5}$米,
∴x2+4x2=45,
解得:x=3,
则AD=6(米),
∵AB=10米,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=8(米),
则BC=8-3=5(米).
故选A.
点评 本题考查了坡度和坡角的知识,解答本题的关键是根据坡度和坡角构造直角三角形以及运用勾股定理求直角三角形的边长.

练习册系列答案
相关题目
16.下列各图中,可围成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
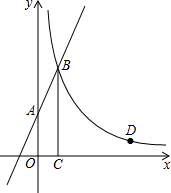 如图,直线y=2x+3与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
如图,直线y=2x+3与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0). 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为4.8cm.
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为4.8cm. (1)计算:$\sqrt{12}$+(-1)2-4cos30°-|$\root{3}{-27}$|
(1)计算:$\sqrt{12}$+(-1)2-4cos30°-|$\root{3}{-27}$|