题目内容
17.解方程组:$\left\{\begin{array}{l}{{x}^{2}-3xy+2{y}^{2}=0}\\{{x}^{2}+{y}^{2}=10}\end{array}\right.$.分析 根据高次方程的解法即可求出答案.
解答 解:由x2-3xy+2y2=0可知:
(x-y)(x-2y)=0
∴x=y或x=2y,
当x=y时,
∴x2+x2=10
∴x=±$\sqrt{5}$,
∴y=±$\sqrt{5}$
当x=2y时,
∴4y2+y2=10,
∴y2=2
∴y=±$\sqrt{2}$,
∴x=±2$\sqrt{2}$,
∴方程组的解为:$\left\{\begin{array}{l}{x=±2\sqrt{2}}\\{y=±\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=±\sqrt{5}}\\{y=±\sqrt{5}}\end{array}\right.$
点评 本题考查高次方程的解法,解题的关键是将高次方程化为低次方程进行解答,本题属于基础题型.

练习册系列答案
相关题目
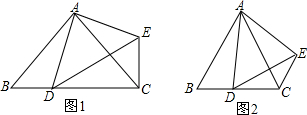 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.



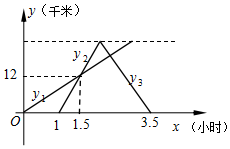 甲乙两人先后由A地沿同一路线前往B地,甲先出发,一小时后乙再出发,半小时后在离A地12千米处乙追上甲,此时两人正好到达AB的中点.然后两人各自保持原速不变,先后到达B地.若甲由A地出发的行驶时间为x小时,甲、乙离开A地的距离为y1千米和y2千米,函数图象如图所示.
甲乙两人先后由A地沿同一路线前往B地,甲先出发,一小时后乙再出发,半小时后在离A地12千米处乙追上甲,此时两人正好到达AB的中点.然后两人各自保持原速不变,先后到达B地.若甲由A地出发的行驶时间为x小时,甲、乙离开A地的距离为y1千米和y2千米,函数图象如图所示.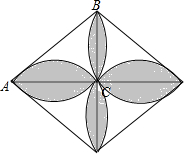 已知,在直角三角形ABC中,∠ACB=90°,AC=8,BC=6,AB=10,以AB边为直径作半圆,把4个相同的直角三角形通过一定的图形运动拼成四叶草的形状(如图所示),求阴影部分的面积.
已知,在直角三角形ABC中,∠ACB=90°,AC=8,BC=6,AB=10,以AB边为直径作半圆,把4个相同的直角三角形通过一定的图形运动拼成四叶草的形状(如图所示),求阴影部分的面积.