题目内容
12.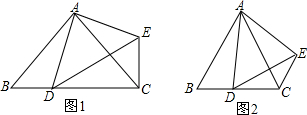 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在直线BC上,如果∠BAC=90°,
求证:CE+DC=BC
证明:∵∠BAC=∠DAE(已知)
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC(已知)}\\{∠BAD=∠CAE(已求)}\\{AD=AE(已知)}\end{array}\right.$
∴△ABD≌△ACE(SAS)
∴BD=CE(全等三角形的对应法相等)
∵BD+DC=BC
∴CE+DC=BC.
(2)如图1,在(1)条件下,求:∠BCE的度数?
(3)如图2,当点D在线段BC上移动,设∠BAC=α,∠BCE=β,则α,β之间有怎样的数量关系?请说明理由.
分析 (1)根据全等三角形的判定方法,补充条件即可解决问题;
(2)由∠BAC=90°,AB=AC,推出∠B=45°,由△ABD≌△ACE,推出∠ACE=∠B=45°;
(3)由∠BAC=α,AB=AC,推出∠B=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α.,由△ABD≌△ACE,推出∠ACE=∠B推出β=90°-$\frac{1}{2}$α;
解答 解:(1):∵∠BAC=∠DAE(已知)
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC(已知)}\\{∠BAD=∠CAE(已求)}\\{AD=AE(已知)}\end{array}\right.$,
∴△ABD≌△ACE(SAS)
∴BD=CE(全等三角形的对应法相等)
∵BD+DC=BC
∴CE+DC=BC.
故答案为ACE,SAS,BD=CE.
(2)∵∠BAC=90°,AB=AC,
∴∠B=45°,
∵△ABD≌△ACE,
∴∠ACE=∠B=45°.
(3)∵∠BAC=α,AB=AC,
∴∠B=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α.,
∵△ABD≌△ACE,
∴∠ACE=∠B
∴β=90°-$\frac{1}{2}$α.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质.三角形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.如果关于x的方程(m+2)x=8无解,那么m的取值范围是( )
| A. | m=-2 | B. | m>-2 | C. | m≠-2 | D. | 任意实数 |
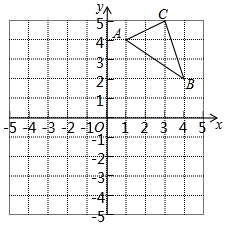 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度). 如图,是用棋子摆成的图形,按照这种摆法,第n个图形中所需棋子的总数是用了n(n+1)个.
如图,是用棋子摆成的图形,按照这种摆法,第n个图形中所需棋子的总数是用了n(n+1)个.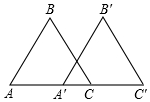 如图,△A′B′C′是由△ABC沿射线AC方向平移20cm得到,若AC=30cm,则A′C=10cm.
如图,△A′B′C′是由△ABC沿射线AC方向平移20cm得到,若AC=30cm,则A′C=10cm.