题目内容
计算：20162－2016×2015.
2016
【解析】试题分析：根据提公因式法分解因式，先确定公因式2016，再提取公因式即可.
试题解析：20162－2016×2015
=2016×（2016-2015）
=2016.
练习册系列答案
阅读快车系列答案
相关题目
如图，在等边△ABC中，P为△ABC内任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，AM⊥BC于M，试猜想AM、PD、PE、PF之间的关系，并说明你的猜想．
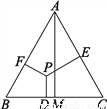
AM＝PD＋PE＋PF，理由见解析
【解析】试题分析：连接AP、BP、CP，根据面积相等，又利用△ABC是等边三角形，即可得PE+PD+PF=AM.
试题解析：PE+PD+PF=AM，理轴如下：
连接AP、BP、CP，
∵S△ABP+S△BCP+S△ACP=S△ABC，
∴AB×PE+BC×PD+AC×PF＝BC×AM，
∵△ABC是等边三角形，
∴AB=... 某市为治理污水，需要铺设一段全长600m的污水排放管道，铺设120m后，为加快施工进度，后来每天比原计划增加20m，结果共用11天完成这一任务，求原计划每天铺设管道的长度．如果设原计划每天铺设xm管道，那么根据题意，可列方程 ．
．
【解析】
试题分析：由题意可得，，化简，得：，故答案为：． 计算：(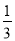
)-1－|－2＋
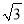tan45°|＋(
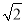－1.41)0＝________.
2＋
【解析】原式＝3－|－2＋|＋1＝4－2＋＝2＋，
故答案为：2+. 为了测量被池塘隔开的A，B两点之间的距离，根据实际情况，作出如图所示的图形，其中AB⊥BE，EF⊥BE，AF交BE于点D，C在BD上．有四位同学分别测量出以下4组数据：①BC，∠ACB；②CD，∠ACB，∠ADB；③EF，DE，BD；④DE，DC，BC.能根据所测数据，求出A，B两点之间距离的有( )
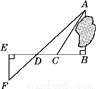
A. 1组 B. 2组 C. 3组 D. 4组
C
【解析】试题分析：此题比较综合，要多方面考虑，
①因为知道∠ACB和BC的长，所以可利用∠ACB的正切来求AB的长；
②可利用∠ACB和∠ADB的正切求出AB；
③因为△ABD∽△EFD可利用，求出AB；
④无法求出A，B间距离．
故共有3组可以求出A，B间距离．
故选C． －3x2＋2x－1＝____________＝－3x2＋_________.
－(3x2－2x＋1) (2x－1)
【解析】根据提公因式的要求，先提取负号，可得－(3x2－2x＋1)，再把2x-1看做一个整体去括号即可得（2x-1）.
故答案为：－(3x2－2x＋1) ，(2x－1). 把a2﹣4a多项式分解因式，结果正确的是（ ）
A. a（a﹣4） B. （a+2）（a﹣2） C. a（a+2）（a﹣2） D. （a﹣2）2﹣4
A
【解析】试题分析： a2-4a=a（a-4），
故选A． 在△ABC中，OE⊥AB，OF⊥AC且OE=OF．
（1）如图，当点O在BC边中点时，试说明AB=AC；
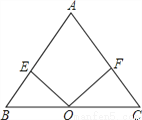
（2）如图，当点O在△ABC内部时，且OB=OC，试说明AB与AC的关系；
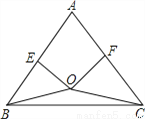
（3）当点O在△ABC外部时，且OB=OC，试判断AB与AC的关系．（画出图形，写出结果即可，无须说明理由）
见解析
【解析】试题分析：（1）证△BOE≌△COF，可得∠B=∠C，通过等角对等边，得出AB=AC；
（2）与（1）类似，在证得△BOE≌△COF后，得∠OBE=∠OCF，OB=OC；则∠OBC=∠OCB，可证得∠ABC=∠ACB，根据等角对等边得出AB=AC；
（3）由前两问的解答过程可知，BC的垂直平分线与∠A的角平分线重合时，AB=AC的结论才成立（等腰三角形三线合一）．... 如果两个图形可以经过平移得到，那么这两个图形的面积 _____.
相等
【解析】试题解析：平移前后的两个图形是全等的，所以面积是相等的.
故答案为：相等.