题目内容
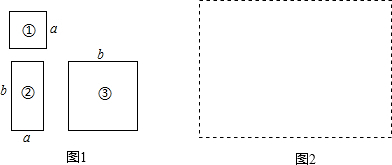
18. 如图,长方形的长AD=9,宽AB=3,则图中阴影部分的面积为9.
如图,长方形的长AD=9,宽AB=3,则图中阴影部分的面积为9.
分析 由图可知,两个阴影部分的面积和正好是一个正方形的面积,由此得解.
解答  解:如图,∵长方形的长AD=9,宽AB=3,
解:如图,∵长方形的长AD=9,宽AB=3,
∴AE=EF=DF=$\frac{1}{3}$AD=3,
∴四边形ABGE,EGHF是正方形,
∴∠A=∠GEF=90°,AB=BF=EF=FC;
故S扇形BAE=S扇形FEG;
∴S阴影=S□EGHF=3×3=9.
故答案为9.
点评 此题主要考查了矩形、正方形的性质以及图形面积的求法;能够发现阴影部分的面积和正方形的面积之间的关系是解答此题的关键.

练习册系列答案
相关题目
9.如果直线y=3x+6与y=2x-4交点坐标为(a,b),则解为$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$的方程组是( )
| A. | $\left\{\begin{array}{l}{y-3x=6}\\{2y+x=-4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-3x=6}\\{2y-x=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{3x-y=6}\\{3x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x-y=-6}\\{2x-y=4}\end{array}\right.$ |
3.把方程8x-1=5x+2移项可得( )
| A. | 8x+5x=2-1 | B. | 8x-5x=-2-1 | C. | 8x-5x=2+1 | D. | 8x+5x=2+1 |
10.若关于x的方程x2+px+q=0(p、q为常数)的两个实数根分别为2和-3,则p、q的值分别为( )
| A. | 2,-3 | B. | -1,-6 | C. | 1,-6 | D. | 1,6 |
7.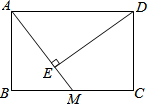 如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
 如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )| A. | 2 | B. | $\frac{12}{5}$ | C. | $\sqrt{13}$ | D. | $\sqrt{5}$ |
8.下列说法正确的是( )
| A. | 4的算术平方根是$\sqrt{2}$ | B. | $\sqrt{16}$的平方根是±2 | ||
| C. | 27的立方根是±3 | D. | $\sqrt{9}$的平方根是±3 |
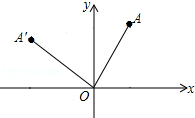 如图,在平面直角坐标系中,已知点A(6,8),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(-8,6).
如图,在平面直角坐标系中,已知点A(6,8),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(-8,6).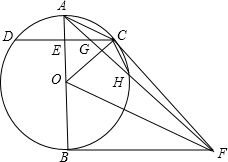 如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连结AF,FC,AF与CD交于点G,与⊙O交于点H,连结CH.
如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连结AF,FC,AF与CD交于点G,与⊙O交于点H,连结CH.