题目内容
8.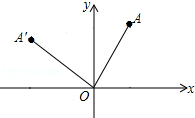 如图,在平面直角坐标系中,已知点A(6,8),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(-8,6).
如图,在平面直角坐标系中,已知点A(6,8),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(-8,6).
分析 过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,根据旋转的性质可得OA=OA′,利用同角的余角相等求出∠OAB=∠A′OB′,然后利用“角角边”证明△AOB和△OA′B′全等,根据全等三角形对应边相等可得OB′=AB,A′B′=OB,然后写出点A′的坐标即可.
解答  解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,
解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,
∵OA绕坐标原点O逆时针旋转90°至OA′,
∴OA=OA′,∠AOA′=90°,
∵∠A′OB′+∠AOB=90°,∠AOB+∠OAB=90°,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
$\left\{\begin{array}{l}{∠OAB=∠A′OB′}\\{∠ABO=∠OB′A′}\\{OA=OA′}\end{array}\right.$,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=8,A′B′=OB=6,
∴点A′的坐标为(-8,6).
故答案为:(-8,6).
点评 本题考查了坐标与图形变化-旋转,正确的作出辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
19.化简($\frac{1}{a}$+$\frac{1}{b}$)÷$\frac{1}{ab}$的结果是( )
| A. | 1 | B. | ab | C. | $\frac{1}{a+b}$ | D. | a+b |
17.若$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是二元一次方程组的解,则这个方程组是( )
| A. | $\left\{\begin{array}{l}{x-3y=5}\\{2x+y=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=5}\\{x+y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=x-3}\\{y-2x=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2y}\\{x=3y+1}\end{array}\right.$ |
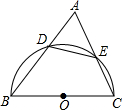 如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC于D,E两点,且cosA=$\frac{\sqrt{3}}{3}$,则S△ADE:S四边形DBCE的值为$\frac{1}{2}$.
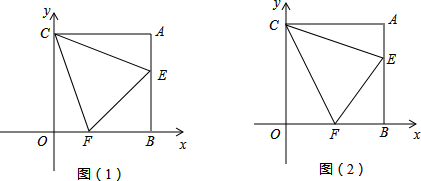
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC于D,E两点,且cosA=$\frac{\sqrt{3}}{3}$,则S△ADE:S四边形DBCE的值为$\frac{1}{2}$. 如图,长方形的长AD=9,宽AB=3,则图中阴影部分的面积为9.
如图,长方形的长AD=9,宽AB=3,则图中阴影部分的面积为9.