题目内容
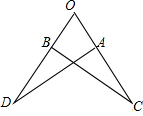 如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若∠O=50°,∠D=35°,则∠OBC等于( )
如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若∠O=50°,∠D=35°,则∠OBC等于( )| A、70° | B、80° |
| C、85° | D、95° |
考点:全等三角形的判定与性质
专题:
分析:由条件可证得△OBC≌△OAD,可得∠C=∠D=35°,在△OBC中利用三角形内角和可求得∠OBC.
解答:解:
在△OBC和△OAD中
∴△OBC≌△OAD(SAS),
∴∠C=∠D=35°,
∵∠O+∠C+∠OBC=180°,且∠O=50°,
∴∠OBC=180°-50°-35°=95°,
故选D.
在△OBC和△OAD中
|
∴△OBC≌△OAD(SAS),
∴∠C=∠D=35°,
∵∠O+∠C+∠OBC=180°,且∠O=50°,
∴∠OBC=180°-50°-35°=95°,
故选D.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法SSS、SAS、ASA、AAS和HL是解题的关键,注意三角形内角和定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
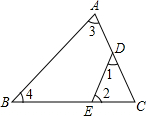 如图,点D,E在△ABC的边上,∠C=50°,则∠1+∠2+∠3+∠4的度数为( )
如图,点D,E在△ABC的边上,∠C=50°,则∠1+∠2+∠3+∠4的度数为( )| A、130° | B、260° |
| C、280° | D、360° |
下列方程中,是一元一次方程的是( )
| A、x2-4x=3 | ||
B、x-1=
| ||
| C、x+2y=3 | ||
| D、x=0 |
数据8,0,2,-4,4的标准差等于( )
A、
| ||
| B、4 | ||
C、
| ||
D、
|
有一个人患了流感,经过两轮传染后新增120个人患了流感,则每轮传染中平均一个人传染人的个数为( )
| A、10 | B、11 | C、60 | D、12 |