题目内容
下列说法中不正确的有( )种.
①在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是9;
②长为7,24,25的三条线段能够组成直角三角形;
③在Rt△ABC中,AC=6,BC=8,则斜边上的中线长为5;
④等腰三角形的两边长是3和5,它的周长是13.
①在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是9;
②长为7,24,25的三条线段能够组成直角三角形;
③在Rt△ABC中,AC=6,BC=8,则斜边上的中线长为5;
④等腰三角形的两边长是3和5,它的周长是13.
| A、1 | B、2 | C、3 | D、4 |
考点:勾股定理的逆定理,三角形三边关系,等腰三角形的性质,直角三角形斜边上的中线,勾股定理
专题:
分析:①由勾股定理可求得AB,再利用面积相等可求得C到AB的距离;②利用勾股定理的逆定理进行判断即可;③条件中没有说明哪条件边为斜边,所以斜边上的中线未发芽等于5;④分腰长为3和5两种情况进行讨论,并利用三角形三边关系进行验证,再求其周长.
解答:解:
∵∠C=90°,AC=9,BC=12,
∴AB=15,
设C到AB的距离为h,则有AB•h=AC•BC,
即15h=9×12,解得h=7.2,
∴C到AB的距离为7.2,
∴①不正确;
∵72+242=625=252,
∴长为7,24,25的三条线段能够组成直角三角形,
∴②正确;
∵在Rt△ABC中,AC=6,BC=8,并未说明哪条边是斜边,
∴斜边上的中线不一定等于5,也可能等于3或4,
∴③不正确;
当腰长为3时,三角形的三边为3、3、5,满足三角形三边关系,此时周长为3+3+5=11,
当腰长为5时,三角形的三边为5、5、3,满足三角形三边关系,此时周长为5+5+3=13,
∴其周长为11或13,
∴④不正确;
综上可知不正确的为①③④,共3个,
故选C.
∵∠C=90°,AC=9,BC=12,
∴AB=15,
设C到AB的距离为h,则有AB•h=AC•BC,
即15h=9×12,解得h=7.2,
∴C到AB的距离为7.2,
∴①不正确;
∵72+242=625=252,
∴长为7,24,25的三条线段能够组成直角三角形,
∴②正确;
∵在Rt△ABC中,AC=6,BC=8,并未说明哪条边是斜边,
∴斜边上的中线不一定等于5,也可能等于3或4,
∴③不正确;
当腰长为3时,三角形的三边为3、3、5,满足三角形三边关系,此时周长为3+3+5=11,
当腰长为5时,三角形的三边为5、5、3,满足三角形三边关系,此时周长为5+5+3=13,
∴其周长为11或13,
∴④不正确;
综上可知不正确的为①③④,共3个,
故选C.
点评:本题主要考查直角三角形的性质及等腰三角形的性质,掌握勾股定理及其逆定理是解题的关键.注意方程思想和分类讨论思想的应用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
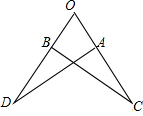 如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若∠O=50°,∠D=35°,则∠OBC等于( )
如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若∠O=50°,∠D=35°,则∠OBC等于( )| A、70° | B、80° |
| C、85° | D、95° |
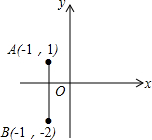 如图,在平面直角坐标系中,已知点A(-1,1),B(-1,-2),将线段AB向下平移2个单位,再向右平移3个单位得到线段A′B′,设点P(x,y)为线段A′B′上任意一点,则x,y满足的条件为( )
如图,在平面直角坐标系中,已知点A(-1,1),B(-1,-2),将线段AB向下平移2个单位,再向右平移3个单位得到线段A′B′,设点P(x,y)为线段A′B′上任意一点,则x,y满足的条件为( )| A、x=3,-4≤y≤-1 |
| B、x=2,-4≤y≤-1 |
| C、-4≤x≤-1,y=3 |
| D、-4≤x≤-1,y=2 |
 数a,b在数轴上的位置如图所示,化简
数a,b在数轴上的位置如图所示,化简