题目内容
已知抛物线与x轴交于m(-1,0),n(3,0),顶点的纵坐标为-8,用三种方法求二次函数的解析式.
考点:待定系数法求二次函数解析式
专题:计算题
分析:第一种方法:设交点式得到y=a(x+1)(x-3),再配成顶点式y=a(x-1)2-4a,然后根据顶点的纵坐标为-8求出a即可;
第二种方法:设抛物线解析式为y=a(x+1)(x-3),利用抛物线的对称性得到抛物线的对称轴为直线x=1,则抛物线顶点坐标为(1,-8),然后把(1,-8)代入所设解析式求出a即可;
第三种方法:利用抛物线的对称性得到抛物线的对称轴为直线x=1,则抛物线顶点坐标为(1,-8),则可设顶点式y=a(x-1)2-8,然后把(-1,0)代入求出a即可.
第二种方法:设抛物线解析式为y=a(x+1)(x-3),利用抛物线的对称性得到抛物线的对称轴为直线x=1,则抛物线顶点坐标为(1,-8),然后把(1,-8)代入所设解析式求出a即可;
第三种方法:利用抛物线的对称性得到抛物线的对称轴为直线x=1,则抛物线顶点坐标为(1,-8),则可设顶点式y=a(x-1)2-8,然后把(-1,0)代入求出a即可.
解答:解:方法一:设抛物线解析式为y=a(x+1)(x-3)=a(x-1)2-4a,
抛物线的顶点坐标为(1,-4a),则-4a=-8,解得a=2,
所以抛物线解析式为y=2(x+1)(x-3)=2x2-4x-6;
方法二:∵抛物线与x轴交于m(-1,0),n(3,0),
∴抛物线的对称轴为直线x=1,
∴抛物线顶点坐标为(1,-8),
设抛物线解析式为y=a(x+1)(x-3),
把(1,-8)代入得a•(1+1)(1-3)=-8,解得a=2,
∴抛物线解析式为y=2(x+1)(x-3)=2x2-4x-6;
方法三:∵抛物线与x轴交于m(-1,0),n(3,0),
∴抛物线的对称轴为直线x=1,
∴抛物线顶点坐标为(1,-8),
设抛物线解析式为y=a(x-1)2-8,
把(-1,0)代入得a•(-1-1)2-8=0,解得a=2,
∴抛物线解析式为y=2(x-1)2-8.
抛物线的顶点坐标为(1,-4a),则-4a=-8,解得a=2,
所以抛物线解析式为y=2(x+1)(x-3)=2x2-4x-6;
方法二:∵抛物线与x轴交于m(-1,0),n(3,0),
∴抛物线的对称轴为直线x=1,
∴抛物线顶点坐标为(1,-8),
设抛物线解析式为y=a(x+1)(x-3),
把(1,-8)代入得a•(1+1)(1-3)=-8,解得a=2,
∴抛物线解析式为y=2(x+1)(x-3)=2x2-4x-6;
方法三:∵抛物线与x轴交于m(-1,0),n(3,0),
∴抛物线的对称轴为直线x=1,
∴抛物线顶点坐标为(1,-8),
设抛物线解析式为y=a(x-1)2-8,
把(-1,0)代入得a•(-1-1)2-8=0,解得a=2,
∴抛物线解析式为y=2(x-1)2-8.
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
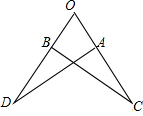 如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若∠O=50°,∠D=35°,则∠OBC等于( )
如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若∠O=50°,∠D=35°,则∠OBC等于( )| A、70° | B、80° |
| C、85° | D、95° |
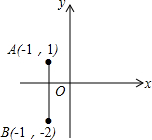 如图,在平面直角坐标系中,已知点A(-1,1),B(-1,-2),将线段AB向下平移2个单位,再向右平移3个单位得到线段A′B′,设点P(x,y)为线段A′B′上任意一点,则x,y满足的条件为( )
如图,在平面直角坐标系中,已知点A(-1,1),B(-1,-2),将线段AB向下平移2个单位,再向右平移3个单位得到线段A′B′,设点P(x,y)为线段A′B′上任意一点,则x,y满足的条件为( )| A、x=3,-4≤y≤-1 |
| B、x=2,-4≤y≤-1 |
| C、-4≤x≤-1,y=3 |
| D、-4≤x≤-1,y=2 |

 数a,b在数轴上的位置如图所示,化简
数a,b在数轴上的位置如图所示,化简