题目内容
因式分解:x2+y2-2xy+4x-4y+4.
考点:因式分解-分组分解法
专题:
分析:将x2+y2-2xy+4x-4y+4中的第一、二、三项结合,四、五项结合,第六项一组,然后进一步分解.
解答:解:x2+y2-2xy+4x-4y+4.
=(x2+y2-2xy)+(4x-4y)+4.
=(x-y)2+4(x-y)+4
=(x-y+2)2
=(x2+y2-2xy)+(4x-4y)+4.
=(x-y)2+4(x-y)+4
=(x-y+2)2
点评:本题考查用分组分解法进行因式分解,关键是正确分组,然后进一步分解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
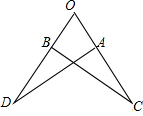 如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若∠O=50°,∠D=35°,则∠OBC等于( )
如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若∠O=50°,∠D=35°,则∠OBC等于( )| A、70° | B、80° |
| C、85° | D、95° |
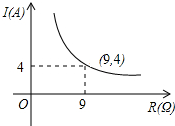 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.