题目内容
6.已知$\frac{1}{x}$+$\frac{1}{y}$=$\frac{1}{6}$,$\frac{1}{y}$+$\frac{1}{z}$=$\frac{1}{9}$,$\frac{1}{z}$+$\frac{1}{x}$=$\frac{1}{15}$,求$\frac{xyz}{xy+yz+zx}$的值.分析 先根据题意得出$\frac{1}{x}$,$\frac{1}{y}$,$\frac{1}{z}$的值,进而可得出$\frac{xy+yz+zx}{xyz}$的值,由此可得出结论.
解答 解:∵$\frac{1}{x}$+$\frac{1}{y}$=$\frac{1}{6}$①,$\frac{1}{y}$+$\frac{1}{z}$=$\frac{1}{9}$②,$\frac{1}{z}$+$\frac{1}{x}$=$\frac{1}{15}$③,
∴①-②+③得,$\frac{1}{x}$=$\frac{11}{180}$,代入①得,$\frac{1}{y}$=$\frac{19}{180}$,把$\frac{1}{y}$=$\frac{19}{180}$代入③得,$\frac{1}{z}$=$\frac{1}{180}$,
∴$\frac{xy+yz+zx}{xyz}$=$\frac{1}{z}$+$\frac{1}{x}$+$\frac{1}{y}$=$\frac{1}{180}$+$\frac{11}{180}$+$\frac{19}{180}$=$\frac{31}{180}$,
∴$\frac{xyz}{xy+yz+zx}$=$\frac{180}{31}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | x2•x3=x6 | B. | x5+x5=2x10 | C. | (-2x)3=8x3 | D. | (-2x3)÷(-6x2)=$\frac{1}{3}$x |
1.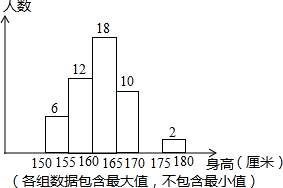 如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
 如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )| A. | 0.36 | B. | 0.46 | C. | 0.56 | D. | 0.6 |