题目内容
14.当-b≤x≤b时,二次函数y=-3x2-3x+4b2+$\frac{9}{2}$的最大值是7,则b=±$\frac{\sqrt{7}}{4}$.分析 首先求得抛物线的对称轴为x=$-\frac{1}{2}$,当|b|<$\frac{1}{2}$时,x=-b时,二次函数有最大值,当|b|≥$\frac{1}{2}$时,x=-$\frac{1}{2}$时,二次函数有最大值,最后根据最大值为7列方程求解即可.
解答 解:抛物线的对称轴为x=$-\frac{1}{2}$,
当|b|<$\frac{1}{2}$时,x=-b时,二次函数有最大值,根据题意得:-3b2+3b+4b2+$\frac{9}{2}$=7,解得:${b}_{1}=\frac{-3+\sqrt{19}}{2}$(舍去),${b}_{2}=\frac{-3-\sqrt{19}}{2}$(舍去);
当当|b|≥$\frac{1}{2}$时,x=-$\frac{1}{2}$时,二次函数有最大值,根据题意得:-3×$\frac{1}{4}$-3×(-$\frac{1}{2}$)+4b2+$\frac{9}{2}$=7.
解得:b=±$\frac{\sqrt{7}}{4}$.
点评 本题主要考查得是二次函数的最值,根据|b|与抛物线的对称轴之间的位置关系进行讨论是解题的关键.

练习册系列答案
相关题目
2.下列事件为必然事件的是( )
| A. | 如果a,b是实数,那么a•b=b•a | |
| B. | 抛掷一枚均匀的硬币,落地后正面朝上 | |
| C. | 汽车行驶到交通岗遇到绿色的信号灯 | |
| D. | 口袋中装有3个红球,从中随机摸出一球,这个球是白球 |
9.一元二次方程x2=2x的根是( )
| A. | x=0 | B. | x=2 | C. | x1=0,x2=2 | D. | 无实数根 |
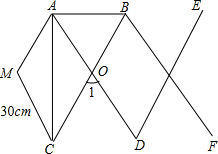 某厂要生产一批边长为30cm的菱形衣帽架(如图),若∠1=60°,则AB,AC的长各是多少?
某厂要生产一批边长为30cm的菱形衣帽架(如图),若∠1=60°,则AB,AC的长各是多少?