题目内容
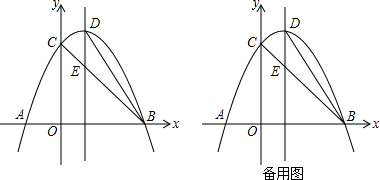
3.如图,抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,对称轴交抛物线于点D、交直线BC于点E,连接DB.(1)求抛物线的解析式;
(2)在对称轴上求一点M,使以C、E、M为顶点的三角形与△BDE相似.
(3)抛物线上是否存在点P,使△PBE与△DBE的面积相等?若存在,求出P点的坐标;若不存在,说明理由.
分析 (1)利用待定系数法求二次函数解析式解答即可;
(2)把二次函数解析式整理成顶点式形式,然后写出点D的坐标,再求出点E的坐标,然后求出DE、BE、CE,再根据相似三角形对应边成比例分两种情况求出EM,然后求出点M到x轴的距离,最后写出点M的坐标即可;
(3)根据等底等高的三角形的面积相等分两种情况求出点P所在的直线,然后与抛物线解析式联立求解即可.
解答 解:(1)将A(-1,0)、B(3,0)、C(0,3)代入抛物线y=ax2+bx+c得,
$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
所以,抛物线解析式为y=-x2+2x+3;
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4),
易求直线BC的解析式为y=-x+3,
当x=1时,y=-1+3=2,
所以,点E的坐标为(1,2),
∴DE=4-2=2,
BE=$\sqrt{(3-1)^{2}+{2}^{2}}$=2$\sqrt{2}$,
CE=$\sqrt{(3-2)^{2}+{1}^{2}}$=$\sqrt{2}$,
①若EM与DE是对应边,则△CME∽△BDE,
所以,$\frac{EM}{DE}$=$\frac{CE}{BE}$,
即$\frac{EM}{2}$=$\frac{\sqrt{2}}{2\sqrt{2}}$,
解得EM=1,
所以,点M到x轴的距离为2-1=1,
所以,点M的坐标为(1,1),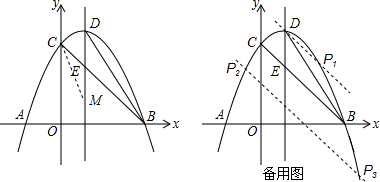
②若EM与BE是对应边,则△MEC∽△BED,
所以,$\frac{EM}{BE}$=$\frac{CE}{DE}$,
即$\frac{EM}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
解得EM=2,
所以,点M的纵坐标为2-2=0,
所以,点M的坐标为(1,0),
综上所述,存在点M(1,0)或(1,1),使以C、E、M为顶点的三角形与△BDE相似;
(3)∵D(1,4),E(1,2),
∴由等底等高的三角形的面积相等可知,要使△PBE与△DBE的面积相等,
过点P的直线与BC平行且经过点(1,4)或(1,0),
易求过(1,4)且与直线BC平行的直线为y=-x+5,
联立$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=-x+5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=4}\end{array}\right.$(为点D的坐标,舍去),$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=3}\end{array}\right.$,
所以,点P的坐标为(2,3),
易求过点(1,0)与直线BC平行的直线为y=-x+1,
联立$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=-x+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{3-\sqrt{17}}{2}}\\{{y}_{1}=\frac{-1+\sqrt{17}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{3+\sqrt{17}}{2}}\\{{y}_{2}=\frac{-1-\sqrt{17}}{2}}\end{array}\right.$,
所以,点P的坐标为($\frac{3-\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$)或($\frac{3+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$),
综上所述,抛物线上存在点P(2,3)或($\frac{3-\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$)或($\frac{3+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$),使△PBE与△DBE的面积相等.
点评 本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,相似三角形的性质,三角形的面积,(2)要分情况讨论是解题的难点,(3)考虑利用等底等高的三角形的面积相等确定出点P所在的直线是解题的关键.

| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | 7 | -3 | 4 | 10 | -9 | -25 |
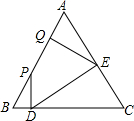 如图,等边△ABC的边长是4,点P是边AB上任意一点(可与A、B重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB的长为x,PQ的长为y,则y与x的函数关系图象是( )
如图,等边△ABC的边长是4,点P是边AB上任意一点(可与A、B重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB的长为x,PQ的长为y,则y与x的函数关系图象是( )| A. | 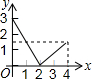 | B. | 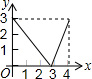 | C. | 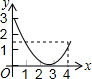 | D. | 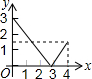 |
| A. | (0,9) | B. | (3,0) | C. | (-3,0) | D. | (3,0)或(3,0) |