题目内容
16.已知函数y=(m+3)xm-2+m2-9,当m为何值时,函数的图象过原点?求此时函数解析式.分析 将点(0,0)代入一次函数解析式y=(m+3)xm-2+m2-9求得m值,利用一次函数的性质知系数m+3≠0求得m值.
解答 解:∵一次函数y=(m+3)xm-2+m2-9的图象过原点,
∴m+3≠0,且m2-9=0,
解得,m=3,
把m=3代入y=(m+3)xm-2+m2-9=6x,
所以函数解析式为:y=6x.
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.某摩托车厂本周计划每日生产250辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日的生产量与计划生产量相比情况如下表(增加的辆数为正,减少的辆数为负)
本周实际总产量是多少?与计划生产量相比,增加了还是减少了?增加或减少多少辆?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | 7 | -3 | 4 | 10 | -9 | -25 |
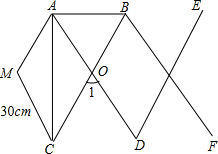 某厂要生产一批边长为30cm的菱形衣帽架(如图),若∠1=60°,则AB,AC的长各是多少?
某厂要生产一批边长为30cm的菱形衣帽架(如图),若∠1=60°,则AB,AC的长各是多少?