题目内容
8. 有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是$\frac{\sqrt{2}}{4}$米.
有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是$\frac{\sqrt{2}}{4}$米.
分析 连接扇形的两个端点,则是直径,因而扇形的半径是2•sin45°=$\sqrt{2}$,扇形的弧长l=$\frac{90π•\sqrt{2}}{180}=\frac{\sqrt{2}π}{2}$,圆锥的底面周长等于侧面展开图的扇形弧长,然后利用弧长公式计算.
解答 解:设底面圆的半径为r,则$\frac{\sqrt{2}π}{2}$=2πr,
∴r=$\frac{\sqrt{2}}{4}$m
圆锥的底面圆的半径长为$\frac{\sqrt{2}}{4}$米,
故答案为:$\frac{\sqrt{2}}{4}$米
点评 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列说法正确的是( )
| A. | 经过一点只能作一条直线 | B. | 射线、线段都是直线的一部分 | ||
| C. | 延长线段AB到点C使AC=BC | D. | 画直线AB=5cm |
3.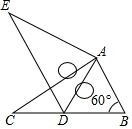 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )| A. | 0.5 | B. | 1.5 | C. | $\sqrt{2}$ | D. | 1 |
13.下列计算正确的是( )
| A. | (2x)2=2x2 | B. | x2•x3=x6 | C. | x5÷x3=x2 | D. | (x-2)3=x-5 |
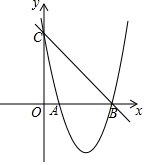 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).